
1. If the curved surface area of the solid sphere is
2. Surface area of the solid hemisphere is 2772sq.cm, then find its total surface area.
Answer
429.6k+ views
Hint: In this problem, we have to find the radius of the sphere whose total surface area given is
Complete step by step solution:
1.Here we have to find the radius of the sphere whose total surface area given is
We know that the formula for the curved surface area of a sphere is
We are already given the value of the curved surface area, which we have to equate to the formula, we get
We can write the
We can now take square root on both sides, we get
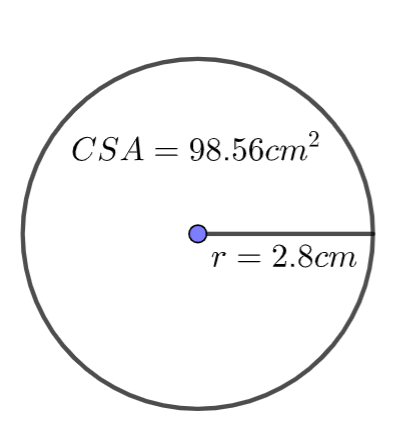
Therefore, the radius is 2.8cm.
2. Here we have to find the total surface area of a solid hemisphere whose curved surface area is 2772sq.cm.
We know that Curved surface area is
We can now take square root on both sides we get
We know that the total surface area of the hemisphere formula is
We can now substitute the value of r in the above formula, we get’
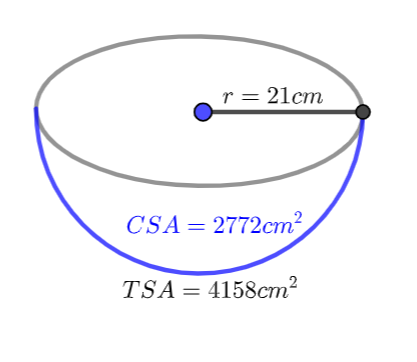
Therefore, the total surface area of the hemisphere is 4158sq.cm.
Note: We should always remember the formulas such as the total surface area of hemisphere formula is
Complete step by step solution:
1.Here we have to find the radius of the sphere whose total surface area given is
We know that the formula for the curved surface area of a sphere is
We are already given the value of the curved surface area, which we have to equate to the formula, we get
We can write the
We can now take square root on both sides, we get

Therefore, the radius is 2.8cm.
2. Here we have to find the total surface area of a solid hemisphere whose curved surface area is 2772sq.cm.
We know that Curved surface area is
We can now take square root on both sides we get
We know that the total surface area of the hemisphere formula is
We can now substitute the value of r in the above formula, we get’

Therefore, the total surface area of the hemisphere is 4158sq.cm.
Note: We should always remember the formulas such as the total surface area of hemisphere formula is
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Differentiate between the Western and the Eastern class 9 social science CBSE




