Question

Given that HCF (306, 657) = 9, find the LCM (306, 657).

Answer 1

Hint: To solve the given question, we will first find out what are the full forms of LCM and HCF and what they actually are. Then, we will write the numbers 306 and 657 as the product of prime numbers. Then we will select the numbers which are common to both 306 and 657. Then we will multiply these selected numbers. The LCM of these two numbers will be a product of these selected numbers and the remaining numbers.

Complete step-by-step answer:
Before, solving the question, we must know what HCF and LCM are. HCF is the short form of the highest common factor. HCF of two or more numbers is the largest positive integer that divides each of the integers. LCM is the short form of the lowest common multiple. LCM of two or more numbers is the smallest positive integer that is divisible by each of the integers. Now, we are asked to find the LCM of 306 and 657. For this, we will do prime factorization of 306 and 657. Thus, the prime factorization of 306 is:

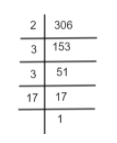
The prime factorization of 657 is:

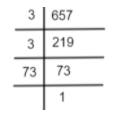
Thus, we can say that,
\[306=2\times 3\times 3\times 17\]
\[657=3\times 3\times 73\]
Here, we can see that the numbers 3 and 3 are common to both 306 and 657. Their product will be \[3\times 3=9.\] Now, we will multiply this product to the remaining numbers which will be equal to the LCM of these two numbers. The remaining numbers are 2, 17, and 73. Thus, the LCM will be
\[LCM=9\times 2\times 17\times 73\]
\[\Rightarrow LCM=22338\]
Thus, LCM of 306 and 657 is 22338.

Note: The alternate method of finding the LCM of 306 and 657 is shown below. We know that if tow positive integers are given then their product will be equal to the product of HCF and LCM of these two integers. Thus, we can say that,
\[LCM\times HCF=\text{ product of numbers}\]
\[\Rightarrow LCM\times 9=306\times 657\]
\[\Rightarrow LCM=\dfrac{306\times 657}{9}\]
\[\Rightarrow LCM=22338\]