Question

5 persons are sitting at a round table in such a way that Tallest person is always on the right side of the shortest person. The number of such arrangements is
A. $6$
B. $8$
C. $24$
D. None of these

Answer 1

Hint: In this problem we need to find the number of possible arrangements that are possible according to the given conditions. We have given that $5$ persons are sitting in a round table and out of them we can observe there is one tall person and one short person. We need to arrange them in an order so that the tallest person is always on the right side of the shortest person. So, we will use the concept of the permutation and use the formulas of permutation to get the required result.

Complete step by step answer:
Given that $5$ persons are sitting at a round table.
From the problem statement we can observe that there should be a tallest person along with the shortest person.
So, we will assume the $5$ persons as $A$, $B$, $C$, $T$, $S$. Where $T$ represents the tallest person and $S$ represents the shortest person.
The arrangement of the $5$ persons in a round table such that tallest person is always right of the shortest person is given by

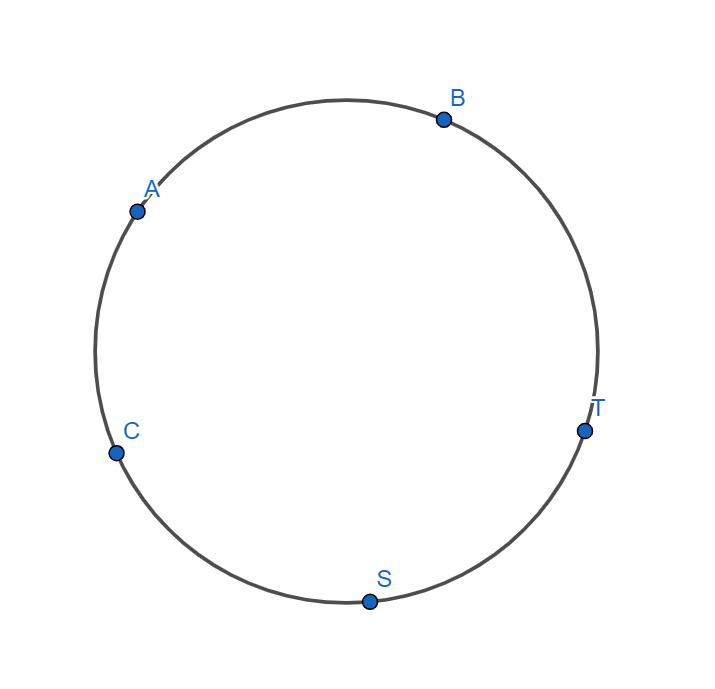
From the above arrangement we can observe that we need to arrange $4$ peoples in a round table.
All similar possible arrangements by using the concept of permutation and combinations are given by
$\left( 4-1 \right)!=3!$
We have the value of $3!$ as $3\times 2\times 1=6$.
Hence the number of possible arrangements is $6$.
So, the correct answer is “Option A”.

Note: In this problem we have given that the people sit in a round table so we have noted the number of possible ways as $\left( n-1 \right)!$. If they have mentioned that the people will sit in a straight table then the number of possible ways is given by $n!$.