
6 tennis balls of diameter 62mm are placed in a cylindrical tube as shown in the figure. Find the volume of the internal unfilled space in the tube and express this as the percentage of the volume of the tube.
Answer
476.7k+ views
Hint: We will find the volume of the tennis balls and the volume of the tube. We will subtract the volume of the tennis balls from the volume of the tube. Then, we will express the volume as the percentage of the volume of the tube by using the formula for percentage.
Formulas used:
1. Volume of a cylinder is given by
2. Volume of a sphere is given by
3. Formula of Percentage is
4.
Complete step-by-step answer:
Each tennis ball is a sphere and the tube is a cylinder.
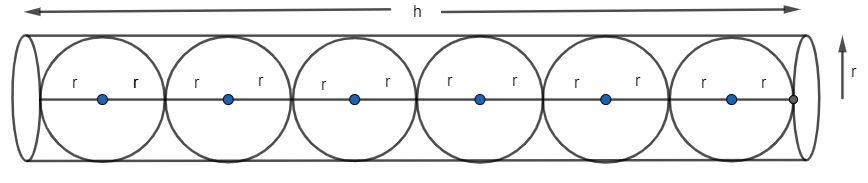
We will calculate the radius of the sphere by substituting 62 for diameter in the formula
The radius of the sphere is 31 mm. We will calculate the volume of the sphere by substituting 31 for
Applying the exponent on the term, we get
Simplifying the above expression, we get
We will calculate the volume occupied by 6 spheres:
We will calculate the volume of the cylinder.
We can see in the figure that the radius of the cylinder is the same as the radius of the sphere and the height of the cylinder is 6 times the diameter of the sphere.
We will substitute 31 for
The volume of internal unoccupied space will be the difference of the volume of the cylinder and the volume of 6 spheres.
Substituting the values of volumes, we get
Subtracting the terms, we get
We will express this volume as a percentage of the volume of the tube. We will substitute 374364.746 for the given volume and 1123094.24 for the total volume in the formula,
Note: We might find it difficult to find the height of the tube. We should look at the figure and geometrically determine the height. The height is 6 times the diameter of a tennis ball or 12 times the radius of the tennis ball.
Formulas used:
1. Volume of a cylinder is given by
2. Volume of a sphere is given by
3. Formula of Percentage is
4.
Complete step-by-step answer:
Each tennis ball is a sphere and the tube is a cylinder.

We will calculate the radius of the sphere by substituting 62 for diameter in the formula
The radius of the sphere is 31 mm. We will calculate the volume of the sphere by substituting 31 for
Applying the exponent on the term, we get
Simplifying the above expression, we get
We will calculate the volume occupied by 6 spheres:
We will calculate the volume of the cylinder.
We can see in the figure that the radius of the cylinder is the same as the radius of the sphere and the height of the cylinder is 6 times the diameter of the sphere.
We will substitute 31 for
The volume of internal unoccupied space will be the difference of the volume of the cylinder and the volume of 6 spheres.
Substituting the values of volumes, we get
Subtracting the terms, we get
We will express this volume as a percentage of the volume of the tube. We will substitute 374364.746 for the given volume and 1123094.24 for the total volume in the formula,
Note: We might find it difficult to find the height of the tube. We should look at the figure and geometrically determine the height. The height is 6 times the diameter of a tennis ball or 12 times the radius of the tennis ball.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




