
A
Answer
492.3k+ views
Hint: Here we should find the dimension of the new cube which is formed by adding the new layer of cubes then with the help of it we will find the number of cubes which is present in the newly formed cube.
Complete step by step answer:
A

That is it contains 5 cubes of
If we add a layer of
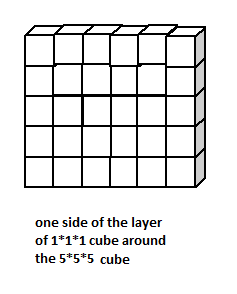
Adding like this layer in image in
That is length
Breadth
Width
Here we add 2 to every dimension because if one cube is added it extends in 2 ways. That is if one cube is added it will increase the length by one and also the breadth by one.
Therefore the newly formed cube is of the dimension
Now to find the number of
We multiply the length breadth and width of the newly formed cube.
The number of
Hence we have found the number of
Note:
Like this problem first, we have to imagine the problem practically. Because thinking like this we will get how the cube will be in the structure. It will help to understand the solution of the problem and more we have to concentrate on calculating the sides of the cube. We may go wrong on that step.
Complete step by step answer:
A

That is it contains 5 cubes of
If we add a layer of

Adding like this layer in image in
That is length
Breadth
Width
Here we add 2 to every dimension because if one cube is added it extends in 2 ways. That is if one cube is added it will increase the length by one and also the breadth by one.
Therefore the newly formed cube is of the dimension
Now to find the number of
We multiply the length breadth and width of the newly formed cube.
The number of
Hence we have found the number of
Note:
Like this problem first, we have to imagine the problem practically. Because thinking like this we will get how the cube will be in the structure. It will help to understand the solution of the problem and more we have to concentrate on calculating the sides of the cube. We may go wrong on that step.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




