Question

A batsman deflects a ball by an angle of ${{90}^{{}^\circ }}$ without changing its initial speed, which is equal to 54 km/ hr. What is the impulse to the ball? Mass of the ball is 0.15 kg.

Answer 1

Hint: We should know that the impulse-momentum theorem states that the change in momentum of an object equals the impulse applied to it. The impulse-momentum theorem is logically equivalent to Newton's second law of motion. Because of the impulse-momentum theorem, we can make a direct connection between how a force acts on an object over time and the motion of the object. One of the reasons why impulse is important and useful is that in the real world, forces are often not constant. Based on this concept we have to solve this question.

Complete step by step answer
The diagram for the question is given below

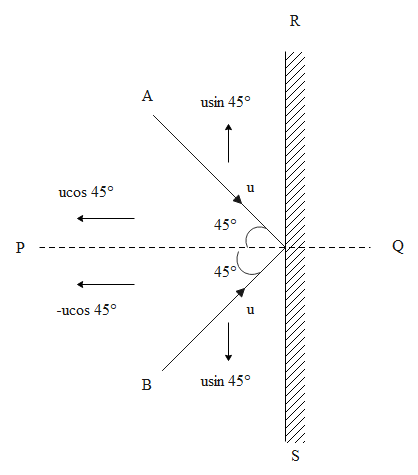
We know that it is given:
Mass of the ball $\mathrm{m}=0.15 \mathrm{kg}$.
 The initial speed of the ball $\mathrm{u}=54 \mathrm{km} / \mathrm{h}=\dfrac{54 \times 1000}{60 \times 60}=15 \mathrm{m} / \mathrm{s}$
The final speed of the ball is given as $\mathrm{v}_{\mathrm{f}}=\mathrm{u} \cos 45^{0}$
The momentum change takes place in the ball in the vertical direction only because the initial and final momentum in the horizontal direction is cancelled out.
Now the expression is given as:
$\mathrm{v}_{\mathrm{i}}=-\mathrm{u} \cos 45^{0}$
According to the impulse-momentum theorem,
 Impulse is equals to Change in momentum
So, the expression becomes:
$\Rightarrow \mathrm{I}=\mathrm{m}\left(\mathrm{v}_{\mathrm{f}}-\mathrm{v}_{\mathrm{i}}\right)$
After the evaluation we get:
$\mathrm{I}=\operatorname{mucos} 45^{0}-\left(-\operatorname{mucos} 45^{0}\right)$
$\mathrm{I}=2 \mathrm{mucos} 45^{0}$
Now we have to substitute the value of mass and velocity to get:
$\mathrm{I}=2 \times 0.15 \times 15 \times 0.7071$
$\mathrm{I}=3.19 \mathrm{kgm} / \mathrm{s}$

Hence the impulse of the ball is 3.19 kgm/s.

Note: We should know that momentum is mass in motion, and any moving object can have momentum. An object's change in momentum is equal to its impulse. Impulse is a quantity of force times the time interval. Impulse is not equal to momentum itself; rather, it's the increase or decrease of an object's momentum. When a net force acts on a body, it produces acceleration in the body and will be equal to rate of change of momentum”. The Newton second law states that the Rate of change of momentum of the body is directly to the force applied in the direction of the applied force.
It should also be known that impulse is an important concept in the study of momentum. An impulse is equal to the net force on the object times the time period over which this force is applied.