
A bimetallic strip is formed out of two identical strips, one of copper and the other of brass. the coefficients of linear expansion of the two metals are ${{\alpha }_{c}}$and ${{\alpha }_{b}}$(${{\alpha }_{b}}>{{\alpha }_{c}}$). On heating the bimetallic strip through temperature $\Delta T$, the strip bends into an arc of a circle. find the radius of curvature of the strip
A. $R=\dfrac{2d}{\left( {{\alpha }_{b}}-{{\alpha }_{c}} \right)\Delta T}$
B. $R=\dfrac{3d}{({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T}$
C. $R=\dfrac{d}{({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T}$
D. $R=\dfrac{d}{2({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T}$
Answer
482.1k+ views
Hint: Bimetallic strips are strips consisting of two different metals having different temperature coefficients. They expand or contract whenever there is change in temperature. Their expansion is governed by a basic law.
Formula used:
$l={{l}_{0}}(1+\alpha \Delta T)$
$l=R\theta $
Complete step by step answer:
Let us consider a strip as described in the question. Let the first layer of the bimetallic strip be of copper and the second layer on the bimetallic strip be of brass. Also, consider the width of the bimetallic strip be $d$.
As we heat the bimetallic strip, it heats up, bends and gets formed into the shape of an arc as shown in the figure.
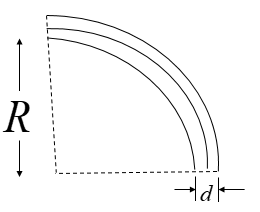
Let the arc formed be a part of a circle with radius $R$
As we know, for a given material, it can be written as
$l={{l}_{0}}(1+\alpha \Delta T)$
Here, the initial length of both the copper and brass layers is the same. Let it be ${{l}_{0}}$
Thus, for copper strip: ${{l}_{c}}={{l}_{0}}(1+{{\alpha }_{c}}\Delta T)$ ---(i)
For brass strip: \[{{l}_{b}}={{l}_{0}}(1+{{\alpha }_{b}}\Delta T)\] ---(ii)
Also, as they are a part of the arc of a circle, we can say that
Arc length = Radius * angle subtended
Thus, for copper:
${{l}_{c}}=R\theta $ ----(iii)
And for brass:
${{l}_{b}}=\left( R+d \right)\theta $ ----(iv)
From equation (i) and (iii)
$R\theta ={{l}_{0}}(1+{{\alpha }_{c}}\Delta T)$ ----(v)
Also, from equation (ii) and (iv)
$(R+d)\theta ={{l}_{0}}(1+{{\alpha }_{b}}\Delta T)$ ----(vi)
Now, (vi)/ (v):
\[\dfrac{(R+d)\theta }{R\theta }=\dfrac{{{l}_{0}}(1+{{\alpha }_{b}}\Delta T)}{{{l}_{0}}(1+{{\alpha }_{c}}\Delta T)}\]
\[\Rightarrow \dfrac{(R+d)}{R}=(1+{{\alpha }_{b}}\Delta T){{(1+{{\alpha }_{c}}\Delta T)}^{-1}}\]
Using Binomial theorem, ${{(1+at)}^{-1}}=1-at$
Here, we get:
\[\Rightarrow \dfrac{(R+d)}{R}=(1+{{\alpha }_{b}}\Delta T)(1-{{\alpha }_{c}}\Delta T)\]
\[\Rightarrow 1+\dfrac{d}{R}=1+({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T+\Delta {{T}^{2}}\]
Here, $\Delta {{T}^{2}}\to \text{very very small}$
So, we neglect it.
\[\Rightarrow \dfrac{d}{R}=({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T\]
$\Rightarrow R=\dfrac{d}{({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T}$
Thus, the correct option is (c).
Note:
Bimetallic strips are predominantly used in some thermostats to measure the change in temperature. Due to the presence of two different metals, they expand or contract at different rates causing the strip to bend. This bend indicates change in temperature.
Formula used:
$l={{l}_{0}}(1+\alpha \Delta T)$
$l=R\theta $
Complete step by step answer:
Let us consider a strip as described in the question. Let the first layer of the bimetallic strip be of copper and the second layer on the bimetallic strip be of brass. Also, consider the width of the bimetallic strip be $d$.
As we heat the bimetallic strip, it heats up, bends and gets formed into the shape of an arc as shown in the figure.

Let the arc formed be a part of a circle with radius $R$
As we know, for a given material, it can be written as
$l={{l}_{0}}(1+\alpha \Delta T)$
Here, the initial length of both the copper and brass layers is the same. Let it be ${{l}_{0}}$
Thus, for copper strip: ${{l}_{c}}={{l}_{0}}(1+{{\alpha }_{c}}\Delta T)$ ---(i)
For brass strip: \[{{l}_{b}}={{l}_{0}}(1+{{\alpha }_{b}}\Delta T)\] ---(ii)
Also, as they are a part of the arc of a circle, we can say that
Arc length = Radius * angle subtended
Thus, for copper:
${{l}_{c}}=R\theta $ ----(iii)
And for brass:
${{l}_{b}}=\left( R+d \right)\theta $ ----(iv)
From equation (i) and (iii)
$R\theta ={{l}_{0}}(1+{{\alpha }_{c}}\Delta T)$ ----(v)
Also, from equation (ii) and (iv)
$(R+d)\theta ={{l}_{0}}(1+{{\alpha }_{b}}\Delta T)$ ----(vi)
Now, (vi)/ (v):
\[\dfrac{(R+d)\theta }{R\theta }=\dfrac{{{l}_{0}}(1+{{\alpha }_{b}}\Delta T)}{{{l}_{0}}(1+{{\alpha }_{c}}\Delta T)}\]
\[\Rightarrow \dfrac{(R+d)}{R}=(1+{{\alpha }_{b}}\Delta T){{(1+{{\alpha }_{c}}\Delta T)}^{-1}}\]
Using Binomial theorem, ${{(1+at)}^{-1}}=1-at$
Here, we get:
\[\Rightarrow \dfrac{(R+d)}{R}=(1+{{\alpha }_{b}}\Delta T)(1-{{\alpha }_{c}}\Delta T)\]
\[\Rightarrow 1+\dfrac{d}{R}=1+({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T+\Delta {{T}^{2}}\]
Here, $\Delta {{T}^{2}}\to \text{very very small}$
So, we neglect it.
\[\Rightarrow \dfrac{d}{R}=({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T\]
$\Rightarrow R=\dfrac{d}{({{\alpha }_{b}}-{{\alpha }_{c}})\Delta T}$
Thus, the correct option is (c).
Note:
Bimetallic strips are predominantly used in some thermostats to measure the change in temperature. Due to the presence of two different metals, they expand or contract at different rates causing the strip to bend. This bend indicates change in temperature.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Glucose when reduced with HI and red Phosphorus gives class 11 chemistry CBSE

The highest possible oxidation states of Uranium and class 11 chemistry CBSE

Find the value of x if the mode of the following data class 11 maths CBSE

Which of the following can be used in the Friedel Crafts class 11 chemistry CBSE

A sphere of mass 40 kg is attracted by a second sphere class 11 physics CBSE

Trending doubts
The combining capacity of an element is known as i class 11 chemistry CBSE

State the laws of reflection of light

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Find the image of the point 38 about the line x+3y class 11 maths CBSE

Distinguish between Mitosis and Meiosis class 11 biology CBSE

What is the difference between homolytic and heterolytic class 11 chemistry CBSE




