
A block of metal of mass 50 gram placed over an inclined plane at an angle of 15 slides down without acceleration. If the inclination is increased by 15, what would be the acceleration of the block?
A.
B. 3
C. 4
D. 5
Answer
465.9k+ views
Hint: On an inclined plane, the net acceleration is not zero; only the perpendicular acceleration is. This is because the normal force is equal to the gravity perpendicular component, so the net force is zero in the perpendicular direction (if not the object would go through the plane or fly off the plane upwards). Calculate friction equates it with Normal Force acting on a body and Then calculates acceleration.
Formula used:
Complete Step-by-Step solution:
The acceleration is given by the acceleration of gravity times the sinus of the angle for a frictionless angle grade incline. "Due to an unbalanced force, objects are known to accelerate down inclined planes. The gravity force (also known as weight) acts in a downward direction; yet the normal force acts perpendicular to the surface in a direction (in fact, normal means "perpendicular").
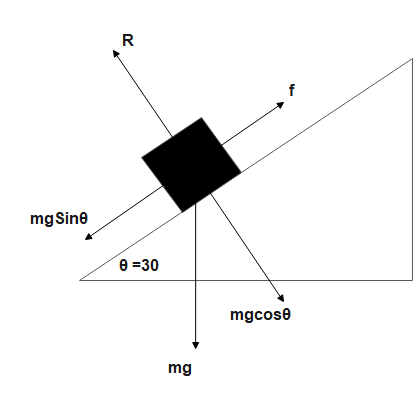
A block of metal of mass
angle of
in equilibrium condition.
e.g., downward force along plane = upward force along plane
we know,
and
so,
now, when inclination increased by
then,
The acceleration of the block be
Note:
Forces are vectors and have a magnitude and a direction. The force of gravity points straight down, but it follows the ramp, but a ball rolling down a ramp doesn't go straight down. The ball is pushed into the ramp by the other component, and the ramp pushes back, so the ball does not accelerate into the ramp. It will accelerate when a rolling object, such as a ball or something on wheels, goes down a hill.
Formula used:
Complete Step-by-Step solution:
The acceleration is given by the acceleration of gravity times the sinus of the angle for a frictionless angle grade incline. "Due to an unbalanced force, objects are known to accelerate down inclined planes. The gravity force (also known as weight) acts in a downward direction; yet the normal force acts perpendicular to the surface in a direction (in fact, normal means "perpendicular").

A block of metal of mass
angle of
in equilibrium condition.
e.g., downward force along plane = upward force along plane
we know,
and
so,
now, when inclination increased by
then,
The acceleration of the block be
Note:
Forces are vectors and have a magnitude and a direction. The force of gravity points straight down, but it follows the ramp, but a ball rolling down a ramp doesn't go straight down. The ball is pushed into the ramp by the other component, and the ramp pushes back, so the ball does not accelerate into the ramp. It will accelerate when a rolling object, such as a ball or something on wheels, goes down a hill.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
The probability that a leap year will have only 52 class 12 maths CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

The final image formed by a compound microscope is class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What are the major means of transport Explain each class 12 social science CBSE

Which of the following properties of a proton can change class 12 physics CBSE




