Question

A body is projected vertically upwards from the surface of the earth with a velocity equal to half the escape velocity. If $R$ is the radius of the earth, the maximum height attained by the body from the surface of the earth is
$\begin{align}
  & \text{A}\text{. }\dfrac{R}{6} \\
 & \text{B}\text{. }\dfrac{R}{3} \\
 & \text{C}\text{. }\dfrac{2R}{3} \\
 & \text{D}\text{. }R \\
\end{align}$

Answer 1

Hint: The minimum speed needed to leave a planet or a moon, means escaping through their gravitational influence, is called escape velocity. The formula for escape velocity comprises gravitational constant, the mass of the body, and distance to the centre of the body. For finding the maximum height obtained by the projected body, we will apply the conservation of total energy at the surface point and at the maximum height.

Formula used:
Expression for escape velocity:
${{V}_{e}}=\sqrt{\dfrac{2GM}{R}}$

Complete step by step answer:
Escape velocity is defined as the minimum amount of speed which is required for a free, non-propelled object to escape from the gravitational influence of a massive body. Escape velocity is a function of the mass of the body and distance to the centre of mass of the body.
Expression for escape velocity:
${{V}_{e}}=\sqrt{\dfrac{2GM}{R}}$
Where,
$G$ is the gravitational constant
$M$ is the mass of the body through which another body is projected
$R$ is the radius of the body through which another body is projected
We are given that a body is projected vertically upwards from the surface of the earth with a velocity equal to half the escape velocity.

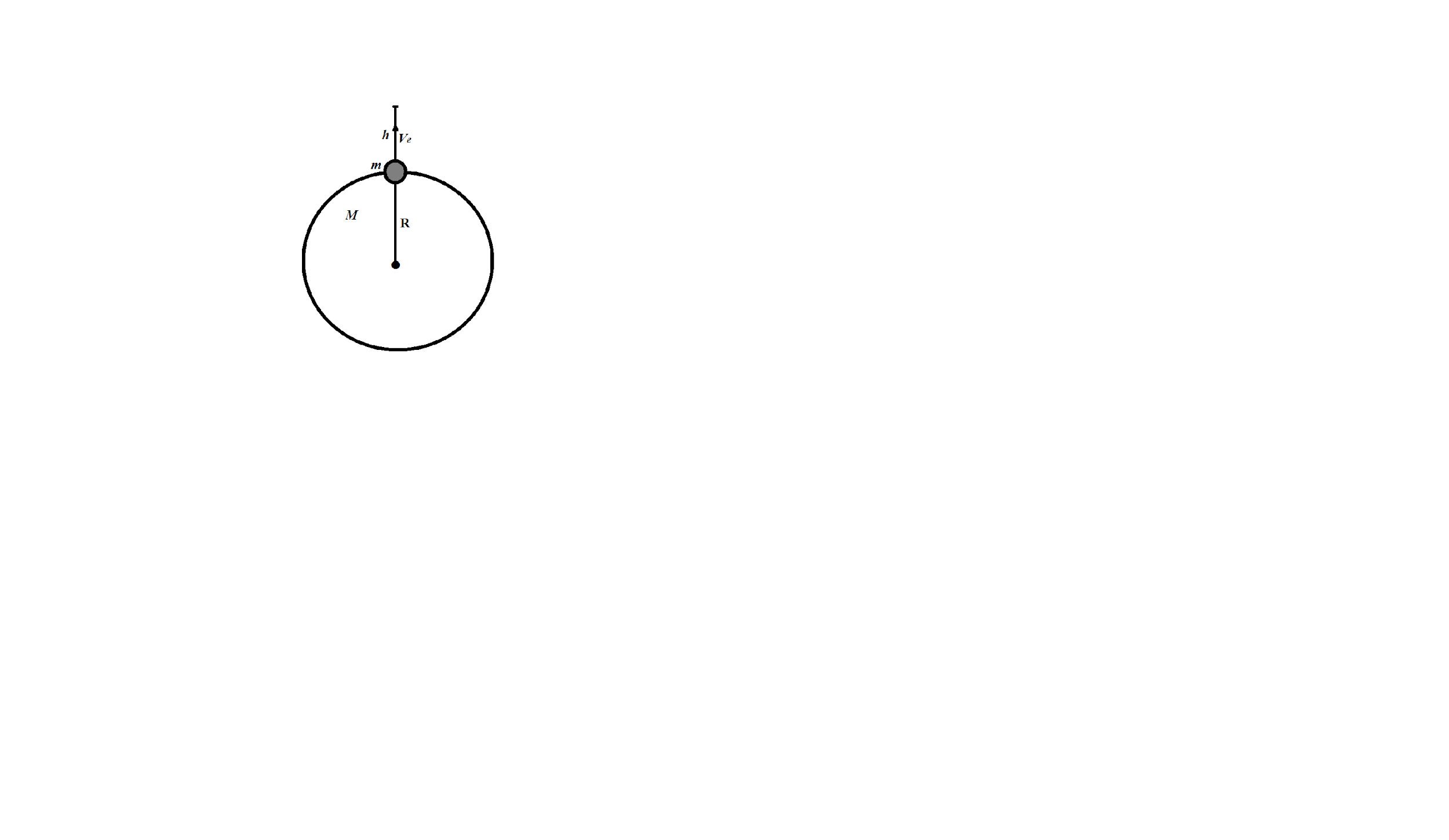
According to the law of conservation of energy,
$T.{{E}_{\text{surface}}}=T.{{E}_{\text{Max height}}}$
The total energy of a body comprises of its Kinetic energy and Potential energy,
$T.E=K.E+P.E$
Total energy at surface of earth is given as,
$\begin{align}
  & T.{{E}_{\text{surface}}}=-\dfrac{GMm}{R}+\dfrac{1}{2}m{{\left( \dfrac{{{V}_{e}}}{2} \right)}^{2}}=-\dfrac{GMm}{R}+\dfrac{1}{2}m{{\left( \dfrac{1}{2}\sqrt{\dfrac{2GM}{R}} \right)}^{2}} \\
 & T.{{E}_{\text{surface}}}=-\dfrac{GMm}{R}+\dfrac{GMm}{4R} \\
 & T.{{E}_{\text{surface}}}=-\dfrac{3GMm}{4R} \\
\end{align}$
Where,
$G$ is the gravitational constant
$M$ is the mass of the body through which another body is projected
$m$ is the mass of the projected body
$R$ is the radius of the body through which another body is projected
Now,
Final energy of the body when it comes to rest is given as,
$T.{{E}_{\text{Max height}}}=-\dfrac{GMm}{R+h}$
$G$ is the gravitational constant
$M$ is the mass of the body through which another body is projected
$m$ is the mass of the projected body
$R$ is the radius of the body through which another body is projected
$h$ is the maximum height attained by the projected body
Kinetic energy at maximum is zero because the body is assumed to come at rest after attaining the maximum height
Now,
Equating the Total energy at the surface with the total energy at maximum height,
$T.{{E}_{\text{surface}}}=T.{{E}_{\text{Max height}}}$
We get,
$\begin{align}
  & -\dfrac{3GMm}{4R}=-\dfrac{GMm}{R+h} \\
 & 4R=3\left( R+h \right) \\
 & 4R=3R+3h \\
 & h=\dfrac{R}{3} \\
\end{align}$
The maximum height attained by the projected body is $\dfrac{R}{3}$
Hence, the correct option is B.

Note:
Students should note here that the escape velocity depends upon the value of gravitational potential at the point from where the body is projected and the maximum height reached by the body. The escape velocity does not depend upon the mass of the projected body, nor does it depend upon the direction of propagation.