
A boiler is in the form of a cylinder 2m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
Answer
518.1k+ views
Hint: In this question we have to find Volume of the boiler. First step is to draw a diagram. It will give us a clear picture of what to find out, considering the given quantity, break the diagram into 3 parts, two hemispheres and one cylinder. Now using the formula of volume of a cylinder and hemisphere you will get the final answer.
Complete step-by-step answer:
According to the question, a boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter.
The height of the cylinder is h and the radius of the cylinder is r.
Height of the cylinder = h = 2 m
Diameter of the hemisphere = 2 m
As we know that Radius =
∴ Radius of the hemisphere =
Since at ends of cylinder hemisphere are attached,
So, Radius of the Cylinder = Radius of the hemisphere = r = 1m
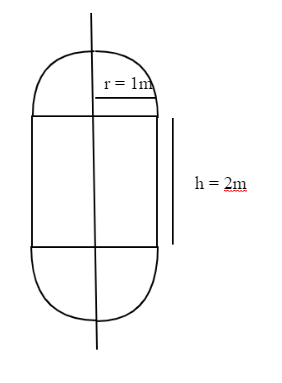
From above diagram,
Total volume of the boiler = Volume of the cylindrical portion + Volume of the two hemispheres
We know that,
Volume of the cylinder =
Volume of the hemisphere =
Now,
Total volume of the boiler =
Therefore, Volume of the boiler is
Note: Whenever we face such types of problems the key concept is to draw the pictorial representation of the given problem and then split into parts such that we can use the formula of standard quantities in order to get the volume of the boiler.
Complete step-by-step answer:
According to the question, a boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter.
The height of the cylinder is h and the radius of the cylinder is r.
Height of the cylinder = h = 2 m
Diameter of the hemisphere = 2 m
As we know that Radius =
∴ Radius of the hemisphere =
Since at ends of cylinder hemisphere are attached,
So, Radius of the Cylinder = Radius of the hemisphere = r = 1m

From above diagram,
Total volume of the boiler = Volume of the cylindrical portion + Volume of the two hemispheres
We know that,
Volume of the cylinder =
Volume of the hemisphere =
Now,
Total volume of the boiler =
Therefore, Volume of the boiler is
Note: Whenever we face such types of problems the key concept is to draw the pictorial representation of the given problem and then split into parts such that we can use the formula of standard quantities in order to get the volume of the boiler.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE




