Question

A charge particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field B, which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
$\begin{align}
  & a)\sqrt{\left( \dfrac{Vm}{q{{B}^{2}}} \right)} \\
 & b)\dfrac{2Vm}{q{{B}^{2}}} \\
 & c)\sqrt{\left( \dfrac{2Vm}{q} \right)}\left( \dfrac{1}{B} \right) \\
 & d)\sqrt{\left( \dfrac{Vm}{q} \right)}\left( \dfrac{1}{B} \right) \\
\end{align}$

Answer 1

Hint: When a charged particle is accelerated through a potential difference of V, it will posses some kinetic energy with its final velocity v. Hence the charged particle will enter the magnetic field with some initial velocity v. Since the direction of motion is perpendicular to the magnetic field the charge will move in a circular path due to the force because of the magnetic field. Hence we can equate the force due to magnetic field i.e. ${{F}_{B}}=q\left( v\times B \right)...(1)$, (where q is the charge of the particle v it its velocity while entering the magnetic field and B is the magnitude of the field) as the centripetal force acting on the charge while moving in circular path given by ${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}...(2)$ where m is the mass of the particle, v is the velocity and r is the radius of the circular orbit. Therefore the radius of the circular path can be calculated from the above expression.

Complete step by step answer:

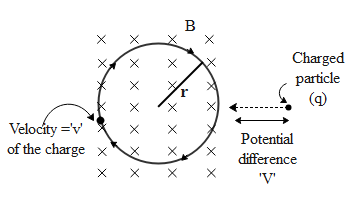
Let us say the charged particle is moved through a potential difference V as seen in the above diagram. Hence the energy possessed by the particle of charge q is given by,
$E=Vq$. This energy of the particle is seen in the form of kinetic energy. Let us say the mass of the charge as m and its final velocity just before entering the field B is v, Therefore,
$\begin{align}
  & K.E=Vq \\
 & \dfrac{1}{2}m{{v}^{2}}=Vq \\
 & \Rightarrow {{v}^{2}}=\dfrac{2Vq}{m} \\
 & \Rightarrow v=\sqrt{\dfrac{2Vq}{m}} \\
\end{align}$
Therefore the particle will enter the magnetic field with velocity v.
In the magnetic field the particle moves in a circular path, hence we can write the magnetic force equals the centripetal force. Therefore using equation 1 and 2 we get,
$\begin{align}
  & {{F}_{B}}={{F}_{C}} \\
 & q\left( v\times B \right)=\dfrac{m{{v}^{2}}}{r} \\
 & qv.B\operatorname{Sin}\theta =\dfrac{m{{v}^{2}}}{r} \\
 & \text{Since }\!\!\theta\!\!\text{ =9}{{\text{0}}^{\text{o}}}\text{ Sin9}{{\text{0}}^{\text{o}}}\text{=1} \\
 & \Rightarrow qB=\dfrac{mv}{r} \\
 & \Rightarrow r=\dfrac{mv}{qB} \\
\end{align}$
Substituting for v in the above equation we get,
$\begin{align}
  & r=\dfrac{m\sqrt{\dfrac{2Vq}{m}}}{qB}=\sqrt{\dfrac{2{{m}^{2}}Vq}{{{q}^{2}}m}}\left( \dfrac{1}{B} \right) \\
 & \Rightarrow r=\sqrt{\dfrac{2mV}{q}}\left( \dfrac{1}{B} \right) \\
\end{align}$
Hence the correct answer to the above question is option c.

Note:
It is to be noted initially the charge was at rest before we actually started it to accelerate across the potential difference V. Hence we could conclude that all the energy will be equal to the difference between the initial and final kinetic energy of the charge. The particle actually starts going in a circular path as the cross product taken between v and B is the curl of two vectors.