Question

A charged particle of mass m and charge q is moved from\[x=0\] by an electric field \[\overrightarrow{E}=\left( {{E}_{0}}-\alpha x \right)\overset{\wedge }{\mathop{i}}\,\] where $\alpha$ is the positive constant and x is the displacement of the particle in time t along x-axis. Find the distance moved by a particle when it is again brought to rest and the acceleration of the particle at that instant. Describe the motion of the particle.

Answer 1

Hint: Here we have given a charged particle which is moved by an electric field and we have to find the distance and the moved by a particle to bring it to rest. And we also have to find the acceleration at that point. For that, we can use the formula of force which is experienced by a charged in an electric field, and by using the same formula we can describe the motion of the particle.
Formula used:
\[\begin{align}
  & F=qE \\
 & F=ma \\
\end{align}\]

Complete step-by-step solution
Here a charged particle is given of mass m and charge q is moved from rest by an electric field \[\overrightarrow{E}=\left( {{E}_{0}}-\alpha x \right)\overset{\wedge }{\mathop{i}}\,\]where $\alpha$ is the positive constant and x is the displacement of the particle in time t along x-axis. And \[{{E}_{0}}\] is the electric field at \[x=0\]. A diagram for this can be given as follows

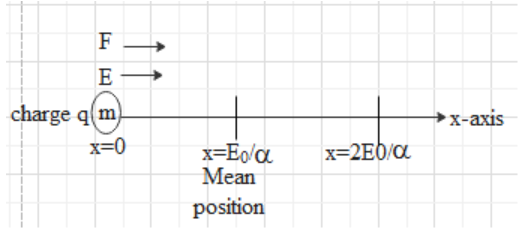
In the above diagram F is the force and we will further discuss the other positions of the x.
 Now we know that the force experienced by an electric charge is given as a product of charge and the electric field, i.e.
\[F=qE\]
Now substituting the given value of E, we get
\[\begin{align}
  & F=q\left( {{E}_{0}}-\alpha x \right)\text{ }..............\text{(i)} \\
 & \Rightarrow F=q{{E}_{0}}-q\alpha x \\
 & \Rightarrow F={{F}_{0}}-q\alpha x \\
 & \Rightarrow F-{{F}_{0}}=-q\alpha x \\
\end{align}\]
Here \[{{F}_{0}}\] is the force experienced by the charge when it is at \[x=0\]. As F and \[{{F}_{0}}\] are both forces at different x, so we can write
\[\begin{align}
  & F'=F-{{F}_{0}} \\
 & \Rightarrow F'=-q\alpha x \\
\end{align}\]
Now from the above equation, we say that F’ is directly proportional to the displacement x
\[F'\propto -x\]
$\alpha$ is a positive constant. This proportionality is for the simple harmonic motion. Hence the motion of the charge will be oscillatory.
For SHM the mean position is where the object is consider to be at rest and so the force at that point will be zero, which gives us
\[\begin{align}
  & q\left( {{E}_{0}}-\alpha x \right)=0 \\
 & \Rightarrow \left( {{E}_{0}}-\alpha x \right)=0 \\
 & \Rightarrow \alpha x={{E}_{0}} \\
 & \Rightarrow x=\dfrac{{{E}_{0}}}{\alpha } \\
\end{align}\]
Now the distance the charge will cover to back to rest or its mean position is twice the mean position. If we say x’ is the distance which the charged particle has to cover to back its mean position, then
\[\begin{align}
  & x'=2x \\
 & \Rightarrow x'=2\left( \dfrac{{{E}_{0}}}{\alpha } \right) \\
\end{align}\]
Now we now that force is given as product of mass and acceleration. It is given that the charged particle has mass m and if a is the acceleration then we can rewrite the equation (i) as
\[ma=q\left( {{E}_{0}}-\alpha x \right)\]
We have to find acceleration when charged particle covers distance x’, so substituting value of x’ in the place of x in the above equation we get
\[\begin{align}
  & ma=q\left( {{E}_{0}}-\alpha \left( \dfrac{2{{E}_{0}}}{\alpha } \right) \right) \\
 & \Rightarrow ma=q\left( {{E}_{0}}-2{{E}_{0}} \right) \\
 & \Rightarrow ma=-q{{E}_{0}} \\
 & \Rightarrow a=-\dfrac{q}{m}{{E}_{0}} \\
\end{align}\]
Negative sign indicates that acceleration is decreasing with distance.
Hence the distance moved by a particle when it is again brought to rest is \[\dfrac{2{{E}_{0}}}{\alpha }\] and the acceleration of the particle at that instant is \[-\dfrac{q}{m}{{E}_{0}}\].
And the particle has oscillatory motion from \[x=0\text{ to }x=\dfrac{2{{E}_{0}}}{\alpha }\].

Note: Every simple harmonic motion is oscillatory motion but it is not necessary that each oscillatory motion is simple harmonic. It was not given that \[{{E}_{0}}\] is the electric field at point \[x=0\] but if we substitute the value of x as zero in the equation given for the electric field then we will get the electric field at \[x=0\] which is \[{{E}_{0}}\].