Question

A circle circumscribed a square of side a centimetre finds the area of the circle.

Answer 1

Hint: The question asks to find the area of a circle in which a square of side $ 1 $ centimetres. The question can be solved by first drawing the relevant figure so as to visualise the problem, the radius of the circle will be found and then we will use the formula given below to find the area of the circle.
 $ A = \pi {r^2} $ ,
Where $ r $ is the radius.

Complete step by step solution:
The square is inscribed in the circle. The side of the square is given as $ 1cm $ . We will first see a diagram of the problem.

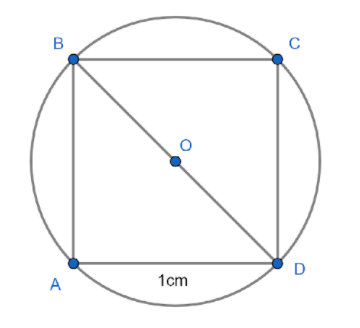
In the diagram we see a circle with centre $ O $ inscribing a square $ ABCD $ of side $ 1cm $ , the diagonal of the circle passes through the centre of the circle, hence we can infer that the segment $ BD $ is the diameter of the circle. Thus we can write that,
 $ diagonal{\text{ }}of{\text{ }}square = diameter{\text{ }}of{\text{ }}circle $
The diagonal of a square is given by,
 $ Diagonal = \sqrt 2 \times side $ ,
Since side is $ 1cm $
The diagonal will be
 $ \Rightarrow diagonal = \sqrt 2 cm $
The diameter will also be the same. The radius of the circle will be given by,
 $ Radius = \dfrac{{Diameter}}{2} $
The radius is therefore calculated as,
 $ \Rightarrow Radius = \dfrac{{\sqrt 2 }}{2}cm $
The area will now be calculated by the formula,
 $ A = \pi {r^2} $ ,
Where $ r $ is the radius.
 $ \Rightarrow A = \pi \times {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} $
 $ \Rightarrow A = \dfrac{\pi }{2} $
 $ \Rightarrow A = \dfrac{{3.14}}{2} $
 $ \Rightarrow A = 1.57{\text{ c}}{{\text{m}}^2} $
Thus we achieve our final result.

Note: An easy way to remember the radius in both the cases when the circle is inscribed or circumscribed with a square of side $ s $ is given below,
When square is inscribed in a circle
 $ R = \dfrac{s}{{\sqrt 2 }} $
Term $ R $ is called circumradius,
When the circle is inscribed in square.
 $ r = \dfrac{s}{2} $
Term $ r $ is also called the inradius.