Question

A conductor in the form of a right angle ABC with $AB=3\;cm$ and $BC=4\;cm$ carries a current of $10\;A$. There is a uniform magnetic field of $5T$ perpendicular to the plane of the conductor. The force on the conductor will be:
A.1.5N
B.2.0N
C.2.5N
D.3.5N

Answer 1

Hint: Recall the expression that is related to the force acting on a current carrying conductor, the applied magnetic field, the current carried by the conductor and the length of the conductor. Using this expression and the fact that force is always perpendicular to the plane containing the current and the applied magnetic field vector, determine the magnitude of force acting along length AB and length BC separately. Then, find the resultant force acting on the entire conductor as a result of these two, and this should lead you right to the solution.

Formula Used:
Force acting on a current carrying conductor placed in a uniform magnetic field B:
$F = I \times Bl = IBlsin\theta$

Complete answer:
We have a conductor as shown the figure.
Both arms of the conductor carry $I = 10\;A$ of current each.
There is a magnetic field $B = 5T$ that is applied in a plane perpendicular to the conductor. This means that the angle between the current flowing through both arms of the conductor and the magnetic field will be $\theta = 90^{\circ} \Rightarrow sin90^{\circ} = 1$. In any case, the force acting on the current carrying conductor can be given as:
$F = IBlsin\theta = 10 \times 5 \times l sin90^{\circ} = 50l\;N$
Let us find the force acting on length AB of the conductor:
$l = 3\;cm \Rightarrow F_{AB} = 50 \times 0.03 = 1.5\;N$
From Fleming’s left hand rule we determine that this force is directed horizontally towards the right of the length of the conductor.

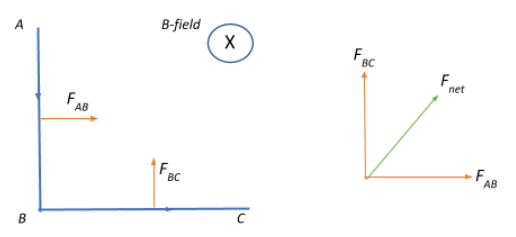
Similarly, we find the force acting on the length BC of the conductor:
$l=4\;cm \Rightarrow F_{BC} = 50 \times 0.04 = 2.0\;N$
Therefore, the resultant force acting on the entire conductor is given as:
$F_{net} = \sqrt{F_{AB}^2 + F_{BC}^2} = \sqrt{1.5^2 + 2^2} = \sqrt{6.25} = 2.5\;N$

Therefore, the correct choice would be C. 2.5N.

Note:
Remember that according to Fleming’s Lefthand Rule, if the thumb, index and the middle fingers are stretched out perpendicular to each other, then the thumb aligns with the direction of force acting on the conductor, the index finger aligns with the direction of the applied magnetic field, and the middle finger gives the current flowing through the conductor. Thus, by knowing the direction of any two of the above quantities, the direction of the third can be easily determined.
Also, do not forget that the force acting on the conductor is always perpendicular to the plane containing the current and the applied magnetic field vectors, which is indicated by the cross product between current I and applied field B : $F = (\vec{I} \times \vec{B})l$.