Question

(a) Consider an arbitrary electrostatic field configuration. A small test charge is placed at a null point (i.e. where E=0) of the configuration. Show that the equilibrium of the test charge is necessarily unstable.
(b) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.

Answer 1

Hint: For the first case move the test charge from the null position and check the total electric flux introduced due to restoring force. For the second case move the charges along the line joining the two charges and along the normal to the joining line. Verify whether it is consistent with Gauss’s law or not.

Complete step by step answer:
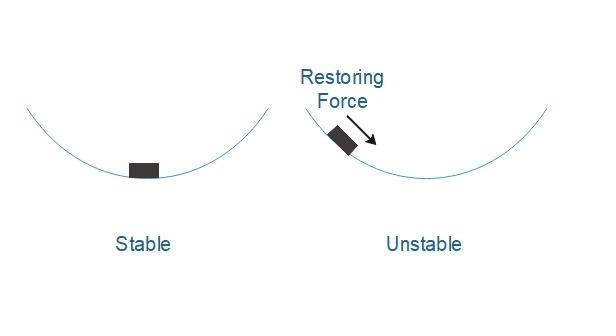
TTo solve this question we first give an analogy of mechanical equilibrium. Consider a bead placed in a bowl. At the center, it will be in an equilibrium state because the net force acting in it will be zero. When you move the bead along the surface in an upward direction a restoring force will act on it and when you release it, we again come back to its original position. In this case, the bead is in a stable equilibrium as it comes to its original position.

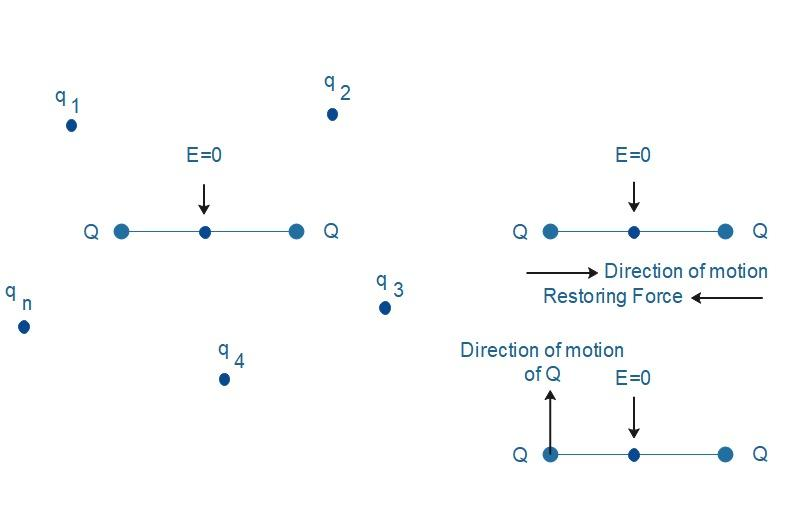
(a) If the test charge is in stable equilibrium then the restoring forces should act in order to bring it to the original position after a slight displacement. Let us assume that the test charge is placed at the null point (i.e. where E=0) is in stable equilibrium. If a test charge is in equilibrium and displaced from its position in any direction, then it experiences a restoring force towards a null point. Thus all the field lines near the null point are directed inward and towards the null point and there is a net inward flux of electric field through a closed surface around the null point. But according to Gauss's law, the net electric flux through a closed surface is equal to total charge within that surface divided by${{\varepsilon }_{0}}$. Here, since there is no charge within the surface the net electric flux must be zero. This means there is restoring force acting on our test charge that will bring it to its original position. But this is a contradiction to our assumption. Hence, the equilibrium of the test charge is necessarily unstable.

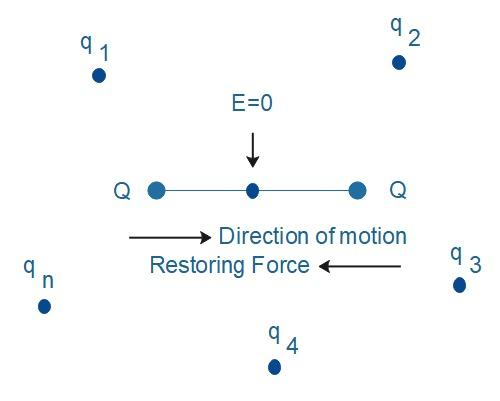
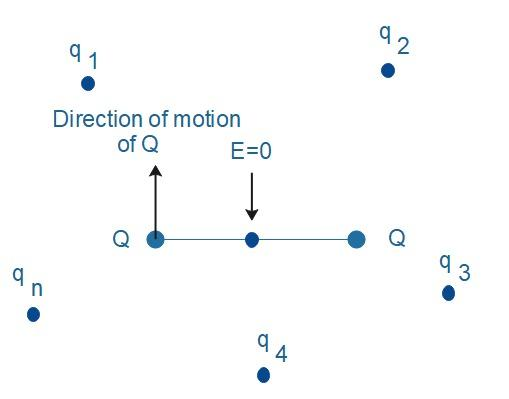
(b) Now if we place two charges of the same magnitude and same sign at a certain distance apart and the null point is the mid-point of the line joining two charges. A restoring force is experienced by the charges when a test charge is displaced along the line. If it is displaced along the normal to the line joining two charges, then the net force takes it away from the null point. Hence, the charge is unstable.

Note:
When a body remains in a particular state then that body is said to be in equilibrium. The equilibrium could be stable or unstable. If the body returns to state even after some disturbances then it is called stable equilibrium and if the body does not return to the state after some disturbances then it is called unstable equilibrium.