Question

A converging beam of light forms a sharp image on a screen. A lens is placed in the path of the beam at $10cm$ from the screen. It is found that the screen has to be moved $8cm$ further away from the lens to obtain a sharp image. Find the focal length and nature of the lens.
A. 12.5 cm
B. 20 cm
C. 13 cm
D. 22.5 cm

Answer 1

Hint:The question involves the concept of lens equation and properly applying standard sign convention and also the concept of initial image acting as a virtual object for obtaining the final sharp image of the screen.
Apply the lens equation for the virtual object with distance from the lens given and its image formed behind the lens at which screen needs to be placed to obtain a sharp image. find the focal length from it and then predict the nature of the lens.

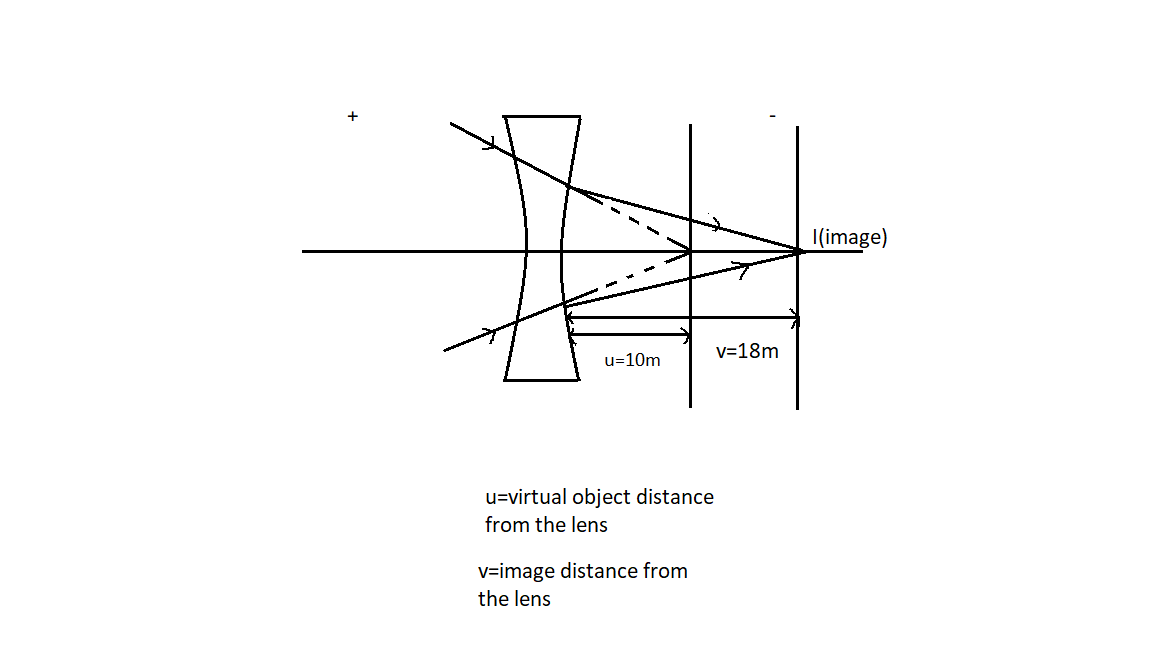
Complete step by step answer:
The rays initially converged at $10m$ behind the lens on the screen. So the initial image will act as a virtual object for the final image $I$ formed at$18m$ from the lens.
The sign convention for object and image is decided by the direction towards which the rays are moving.
The left part in the figure is standardized to positive and the right part as negative.
The lens equation is as follows,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
Where$f$ is focal length, $u$ is the object distance and $v$is the image distance from the pole of the lens.
According to above information,
Virtual Object distance$\left( u \right)$=where initially rays converged=
Image distance=$+\left( 10+8 \right)m$
Putting values in lens equation,
$\Rightarrow \dfrac{1}{f}=\dfrac{1}{18}-\dfrac{1}{10}$
$\Rightarrow \dfrac{1}{f}=-\dfrac{8}{180}m$
$\Rightarrow f=-\dfrac{180}{8}=-22.5m$
The focal lens is negative which means a diverging lens which is a concave lens.

Hence the correct option is D.

Note:
There are many applications of both types of lenses in different areas.
Concave lenses are used to correct nearsightedness. Compound microscopes and telescopes use both convex and concave lenses.
Using combinations of convex lenses may create blurry images. A concave eyepiece is used to correct this problem. The use of concave lenses is essential in lasers.