Question

A convex glass lens has been immersed in water. Compared to its power in air, its power in water will be given as,
A. increase
B. decrease
C. not change
D. decrease for red light and increase for violet light

Answer 1

Hint: The power of a lens can be described as the reciprocal of the focal length of the lens. As the refractive index of water is higher than that of the air, there is a drastic change in the characteristics of lenses which can be understood using the lens maker's equation. These all may help you to solve this question.

Complete answer:
As we all know the power of a lens is found by taking the reciprocal of the focal length. This can be written as,
$P=\dfrac{1}{f}$
Where $f$ be the focal length of the lens.
Using the lens maker's equation, we can write that,
$\dfrac{1}{f}=\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
As per the question mentions, the lens has been immersed inside the water. The refractive index of the water can be written as,
${{\mu }_{water}}=\dfrac{4}{3}$
Whereas the refractive index of the air is,
${{\mu }_{air}}=1$
As the lens is dipper in water the refractive index of the medium gets increased. There the term, $\dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}$ will get decreased. Therefore the $\left( \dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}-1 \right)$ will also get decreased. This will cause the decrease of $\dfrac{1}{f}$. Hence the power will be decreased because of the relation,
$P=\dfrac{1}{f}$
Therefore as the lens is immersed in water, the power of the lens is getting decreased.

Hence the correct answer is option B.

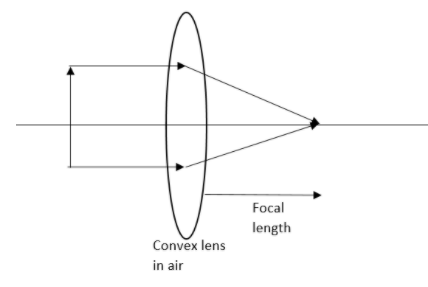
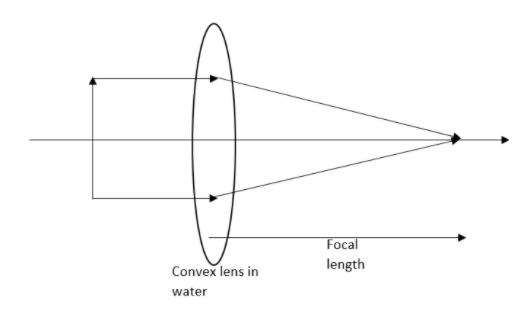
Note: Power of a lens is measured in dioptres. As the convex lenses are having positive focal length, they are having positive power. And as the concave lenses are having a negative focal length, they are found to be with negative power.