Question

A convex lens is put $10\,cm$from a light source and it makes a sharp image on a screen, kept $10\,cm$ from the lens. Now a glass block (refractive index 1.5) of $1.5\,cm$ thickness is placed in contact with the light source. To get the sharp image again, by what distance the screen must be shifted?
A. $0.55\,cm$ away from the lens
B. $1.1\,cm$ away from the lens
C. $0.55\,cm$ towards from the lens
D. 0

Answer 1

Hint: Use lens formula to obtain focal length of the convex lens. When a glass slab is inserted between the path of light rays and convex lens, the object for convex lens appears to be shifted by a distance equal to lateral shift. Again use lens formula to obtain image distance. Take the difference between the newer and earlier position of the image. This is the distance the screen must be shifted to get the sharp image again.

Formula used:
Lens formula, $\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$; Lateral shift due to a slab, $s=t\left( 1-\dfrac{1}{\mu } \right)$

Complete step by step answer:
Initially, light source is at distance $u=-10cm$ from convex lens and image distance $v=10cm$. We use lens formula to obtain focal length of the convex lens. Lens formula is
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$ where $f,v$ and $u$ denotes focal length, image distance and object distance respectively.

                          Fig: Formation of image, initial condition
$\dfrac{1}{f}=\dfrac{1}{10}-\dfrac{1}{-10}=\dfrac{2}{10}$
This implies that, $f=5\,cm$
When a glass slab is inserted between the path of light rays and convex lens, the object for convex lens appears to be shifted by a distance equal to lateral shift.

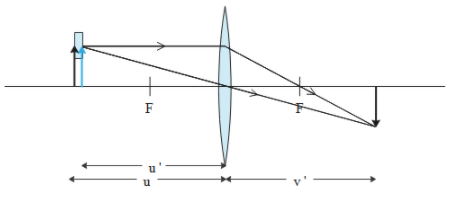
                         Fig: Formation of image, Final condition
Lateral shift, $s=t\left( 1-\dfrac{1}{\mu } \right)$ where $t$ and $\mu$ is the thickness and refractive index of glass slab.
Substituting $t=1.5\,cm$ and $\mu =1.5$, we get
$s=1.5\left( 1-\dfrac{1}{1.5} \right)=0.5cm$
Then, new object distance,
$u'=-10+0.5=-9.5cm$
Using lens formula
$\dfrac{1}{f}=\dfrac{1}{v'}-\dfrac{1}{u'}$
$\Rightarrow \dfrac{1}{5}=\dfrac{1}{v'}-\dfrac{1}{-9.5}\Rightarrow \dfrac{1}{v'}=\dfrac{1}{5}-\dfrac{1}{9.5}$
From this we get
$v=\dfrac{47.5}{4.5}=10.55cm$
Therefore shift in image is
$10.55-10=0.55cm$
Therefore, we need to shift the screen by $0.55\,cm$ away from the convex lens to obtain a sharp image again.

Hence, A is the correct option.

Note:
In mirror as well as optical lens problems, the most important thing to consider is sign conventions. Therefore, students should understand the sign conventions properly and then proceed with the solution. Diagrams are very helpful in understanding the sign conventions.
Focal length of a convex lens is always taken to be positive.