
A cubic foot of water is poured into a rectangular aquarium with base 15 inch by 18 inch. To what height in inches does the water rise.
(a)
(b) 6
(c)
(d)
(e) 5
Answer
501.9k+ views
Hint: First, the condition given in the question is that the aquarium is
Complete step-by-step answer:
In this question, we are supposed to find the height of the rectangular aquarium which is actually a cuboid of length 18 inch, breadth 15 inch and height as h.
So, the figure to show these dimensions is as:
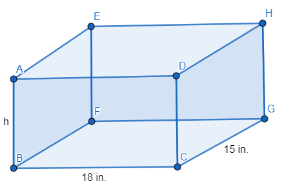
Now, the condition given in the question is that the aquarium is
But, all the dimensions are given in inches, so we need to convert the volume of the aquarium into units of inches.
Then, we know by the relation as:
So, the volume(V) of the aquarium inch inches comes out to be:
Now, we also know the formula to calculate the volume of aquarium which is actually a cuboid as:
So, by substituting the value of l, b and equating it with the above volume, we get:
So, by solving the above equation, we can get the height to which water rises as:
So, the height of the aquarium is
Hence, option (a) is correct.
Note: In these type of questions, firstly we should know some of the conversions such that we are very comfortable in converting them to desired units as:
Secondly, we must know the basic formulas of the 3D figures as:
Volume of cuboid as
Complete step-by-step answer:
In this question, we are supposed to find the height of the rectangular aquarium which is actually a cuboid of length 18 inch, breadth 15 inch and height as h.
So, the figure to show these dimensions is as:

Now, the condition given in the question is that the aquarium is
But, all the dimensions are given in inches, so we need to convert the volume of the aquarium into units of inches.
Then, we know by the relation as:
So, the volume(V) of the aquarium inch inches comes out to be:
Now, we also know the formula to calculate the volume of aquarium which is actually a cuboid as:
So, by substituting the value of l, b and equating it with the above volume, we get:
So, by solving the above equation, we can get the height to which water rises as:
So, the height of the aquarium is
Hence, option (a) is correct.
Note: In these type of questions, firstly we should know some of the conversions such that we are very comfortable in converting them to desired units as:
Secondly, we must know the basic formulas of the 3D figures as:
Volume of cuboid as
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




