Question

A cubical block of side 7 cm is surmounted by a hemisphere of diameter equal to the side of the cube. Find the surface area of the solid.

Answer 1

Hint: In this question, we need to determine the surface area of the solid such that a cubical box is surmounted by a hemisphere. To find the total surface area of the solid surmounted by the hemisphere can be calculated by finding the surface area of the cube then subtract the surface area of the base of the hemisphere then add the surface area of the hemisphere.

Complete step by step solution:
The following figure depicts the data given in the question but in a 2-dimensional way.

Where, 7 cm is the length of the sides of the cubical box and 7 cm is the diameter of the hemi-sphere surmounted on the cubical box.
The greatest diameter = side of the cube = 7cm.

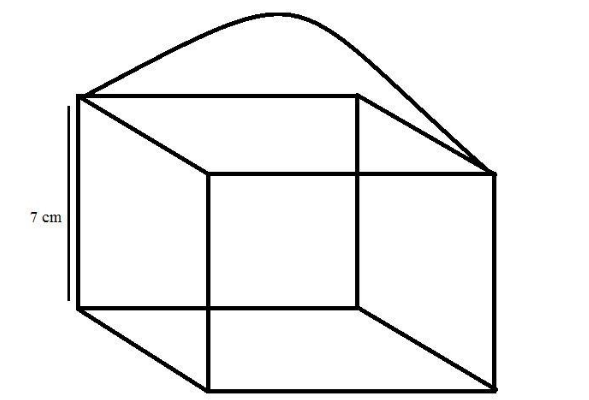
The radius of the hemisphere is given as the half of the diameter of the hemisphere which is 7 cm. So, the radius of the hemi-sphere is 3.5 cm.
Now, the total surface area of the solid framed on surmounting a hemi-sphere on the cube is the difference between the sum of the surface area of the cube and the hemi-sphere and the area of the base of the hemi-sphere. Mathematically,
Surface Area of Solid = Surface Area of Cube - Surface Area of Base Hemisphere + Curved Surface Area of Hemisphere
Surface Area of the Cube is given as 6 times the square of the length of the side. Mathematically, $ {S_{cube}} = 6 \times {\left( {side} \right)^2} $ . Substituting the value of the side as 7, we get
 $
  {S_{cube}} = 6 \times {\left( {side} \right)^2} \\
   = 6 \times {\left( 7 \right)^2} \\
   = 6 \times 9 \\
   = 294\;c{m^2} \\
  $
Surface area of the hemi-sphere is given as $ 2\pi $ times the square of the radius of the hemisphere. Mathematically, $ {S_{hemisphere}} = 2\pi {r^2} $ . Substituting the value of the radius of the hemisphere as 3.5 cm, we get
 $
  {S_{hemisphere}} = 2\pi {r^2} \\
   = 2 \times \dfrac{{22}}{7} \times {\left( {3.5} \right)^2} \\
   = 77\;c{m^2} \\
  $
Now, the area of the base of the hemisphere is given as $ \pi $ times of the square of the radius of the hemisphere. Mathematically, $ {A_{base - hemisphere}} = \pi {r^2} $ . Substituting the value of the radius of the hemisphere as 3.5 cm, we get
 $
  {A_{base - hemisphere}} = \pi {r^2} \\
   = \dfrac{{22}}{7} \times {\left( {3.5} \right)^2} \\
   = 38.5\;c{m^2} \\
  $
 Substituting the value of all the evaluated value in the equation, $ S = {S_{cube}} + {S_{hemisphere}} - {A_{base - hemisphere}} $ , we get
 $
  S = {S_{cube}} + {S_{hemisphere}} - {A_{base - hemisphere}} \\
   = 294 + 77 - 38.5 \\
   = 332.5\;c{m^2} \;
  $
Hence the total surface area of the solid is 332.5 square centimeters.
So, the correct answer is “ 332.5 square centimeters”.

Note: It is interesting to note here that the area of the base of the hemisphere has been subtracted from the summation of the surface area of the cube and the hemisphere as that area will be hidden due to surmounting of the hemi-sphere on the cube. So, students do not forget to exclude the area of the base circle of the hemisphere because otherwise this area will be counted for two times.