Question

A cubical box has an edge 10cm and another cuboidal box is 12.5cm long, 10cm wide and 8cm high. Which box has the greater lateral surface area and by how much?

Answer 1

Hint:Lateral means vertical, so lateral surface area of cube and cuboid can be given by relation \[{{4l}^{2}}\] and \[2h\left( l+b \right)\] respectively, where a is the side of cube and l, b, h are length, breadth and height of cuboid. Areas of upper and lower faces will not be included in lateral surface area.

Complete step by step answer:
As we know the lateral surface area of a cube and cuboid is the sum of the area of walls i.e. area of the four faces (leaving area of upper face and lower face). In other words lateral surface area is the total area leaving the upper and lower face of the cube and cuboid.
Hence, we can get area of cube as

So, lateral surface area = Area of four.
Faces (vertical/ lateral) = \[a\times a+a\times a+a\times a+a\times a=4{{a}^{2}}\].
Where, we know the area of a square = \[{{\left( side \right)}^{2}}\].
Hence, lateral / vertical surface area of the cubical box can be given as,
Lateral surface area of cubical box = \[4\times {{\left( 10 \right)}^{2}}=400c{{m}^{2}}\].
Where the side of the cubical box = 10cm.
Now, similarly we can get lateral surface area of a cuboid as

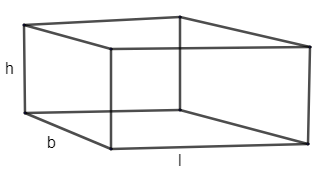
Where l = length
b = breadth
h = height
Now, we area of a rectangle can be given as,
Area of a rectangle = length \[\times \]breadth
Hence, lateral surface area of cuboid can be calculated as
Lateral surface area of a cuboid \[=b\times h+l\times h+b\times h+l\times h\].
\[\Rightarrow \]Lateral surface area of a cuboid =\[2lh+2bh\].
\[\Rightarrow 2h\left( l+b \right)\]
Hence we can calculate area of the given cuboidal box as
Area of the cuboidal box \[=2\times 8\left( 12.5+10 \right)\].
Where, length = 12.5cm
Breadth = 10cm
Height = 8cm
Hence, we get
Area of the cuboidal box = \[16\times 22.5=360.0c{{m}^{2}}\].
Now, we know the lateral surface area of the cubical box and cuboidal box are \[400c{{m}^{2}}\] and \[360c{{m}^{2}}\] respectively. Hence, cubical boxes have greater lateral surface area than cuboidal boxes.
And hence, we can calculate the value by which the lateral surface area of the cubical box is greater than the cuboidal box by taking the difference between them.
Difference between areas = 400 – 360 = \[40c{{m}^{2}}\].
Hence, the cubical box has \[40c{{m}^{2}}\] more lateral surface area than the cuboidal box.

Note: One may get confused with the term lateral surface area. He/ She may use \[6{{a}^{2}}\] and \[2\left( lb+bh+hl \right)\] formulae for calculating lateral surface area of the cube and cuboid respectively which is wrong. Lateral means vertical, so we need an area of 4 faces only and don’t need to include areas of upper and lower faces. So, be clear with the terminologies.