Question

A cubical sealed vessel with edge L is placed on a cart, which is moving horizontally with an acceleration a as shown in the figure. The cube is filled with an ideal fluid having density $\rho $. Find the gauge pressure at the centre of the cubical vessel.

A. $\dfrac{L}{2}\rho g$
B. $\dfrac{L}{2}\rho (g + a)$
C. $\dfrac{L}{2}\rho a$
D. $\dfrac{L}{2}\rho (g - a)$

Answer 1

Hint-When we need to find the pressure at a point inside we can obtain it by writing the equation of successive increase in pressure from one point to another and then from there to another and so on till we reach the required point. We are asked to find the pressure at the centre. So it is at a depth $\dfrac{L}{2}$ from top and horizontal distance $\dfrac{L}{2}$ from the front side.

Step by step solution:
It is given that a cubical sealed vessel is placed on a cart which is moving with an acceleration a. It is filled with fluid of density $\rho $ . We need to find the pressure at the centre of the vessel.
Here, since the vessel is sealed there is no part of fluid exposed to the atmosphere. Therefore, the least pressure point will be the point at the top right corner of the vessel. This is due to the fact that the acceleration due to gravity acts downwards and there is a pseudo acceleration due to the acceleration of the cart acting backwards. Analyze the figure given below.

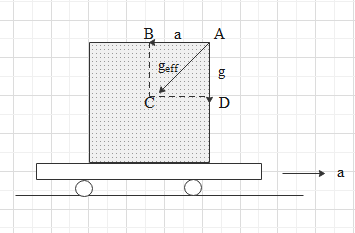
Net acceleration acts in the direction shown. Thus the pressure starts increasing from the top right corner A. So, we can take the pressure at this point to be zero.
Whenever we need to find the pressure at a point inside we can obtain it by writing the equation of successive increase in pressure from one point to another and then from there to another and so on till we reach the required point.
If we want to find pressure at any point inside the fluid which is at a depth h below from the top and at a distance x from the front side we can use the success increment of pressure method. Using this method the pressure at depth h will be $0 + h\rho g$. Because only gravity acts in the vertical direction. Pressure at a horizontal distance l from the front side will be $x\rho a$. Because only pseudo acceleration acts in the horizontal direction. So the net pressure at the point will be the sum of these two pressures.
$P = 0 + h\rho g + x\rho a$
In our case we need to calculate the pressure from A to D and then move left from D to C. so that we reach the centre.
So, the depth is $\dfrac{L}{2}$ since the side of the cube is L centre is at a depth which is half of the distance from top. and the horizontal distance is also $\dfrac{L}{2}$ . let us substitute these values in the above equation. Then we get
Pressure at the centre as
$P = 0 + \dfrac{L}{2}\rho g + \dfrac{L}{2}\rho a$
$\therefore P = \dfrac{L}{2}\rho (g + a)$

So the correct answer is option B

Note:If we calculate the successive increase in pressure by first going from A to B and then from B to C. Then also we will get the same answer. Because the pressure increase from A to B is $\dfrac{L}{2}\rho a$ since pseudo acceleration is taken in horizontal direction. And pressure increase from B to C is $\dfrac{L}{2}\rho g$ since gravity is taken in a vertical direction.
So the net pressure will be $P = \dfrac{L}{2}\rho (g + a)$