Question

(a) Define electric dipole moment. Is it a scalar or vector?
Derive the expression for the electric field of a dipole at a point on the equatorial plane of
the dipole
(b) Draw the equipotential surface due to an electric dipole. Locate the points where the
potential due to the dipole is zero.

Answer 1

Hint: Electric Dipole moment is the measure of the polarity of the system. It is the separation of positive charge and a negative charge by a distance. The SI unit of electric dipole moment is Coulomb-meter. The simplest example is a pair of electric charges of two opposite signs and equal magnitude separated by distance.

Complete Step by Step Solution:
(a) Electric dipole moment- The strength of the electric dipole is measured by the quantity of electric dipole moment. Its magnitude equal to the product of the magnitude of their charge and the distance between the two charges
Electric dipole moment.
$ p = q \times d $
Electric dipole moment is a vector quantity and it is represented as $ \overrightarrow p = q \times \overrightarrow d $ in vector form.
Here p is the dipole moment, q is the charge and d is the distance and direction of $ \overrightarrow d $is from negative charge to positive charge.

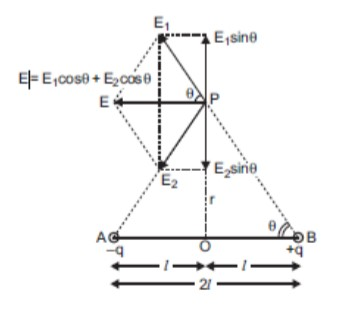
Electric Field of dipole at points on the equatorial plane
Let the magnitude of the electric field due to the two charges +q and -q are given by $E_1$ and $E_2$ respectively.
Therefore from the figure, we have
\[AP = BP = \sqrt {{r^2} + {l^2}} \]
\[\therefore \overrightarrow {E_1} = \dfrac{1}{{4\pi \varepsilon o}}\dfrac{q}{{{r^2} + {l^2}}}\],
along B to P
\[\therefore \overrightarrow {E_2} = \dfrac{1}{{4\pi \varepsilon o}}\dfrac{q}{{{r^2} + {l^2}}}\],
along P to A
Hence both $E_1$ and $E_2$ are equal in magnitude.
Now, to find the resultant electric field, we have to resolve the components along and perpendicular to AB
The components perpendicular to AB are sine components and being equal and opposite to each other they cancel out each other.
Therefore the resultant electric field is given by,
$
E_1 = E_1\cos \theta + E_2\cos \theta \\
But, \\
E_1 = E_2 = \dfrac{1}{{4\pi \varepsilon o}}\dfrac{q}{{{r^2} + {l^2}}} \\
 $
Thus clearly we can say that
$
\cos \theta = \dfrac{{OB}}{{PB}} = \dfrac{l}{{\sqrt {{r^2} + {l^2}} }} = \dfrac{l}{{{{({r^2} +
{l^2})}^{1/2}}}} \\
\therefore E = 2E_1\cos \theta \\
= 2 \times \dfrac{1}{{4\pi \varepsilon o}}\dfrac{q}{{({r^2} + {l^2})}}\dfrac{l}{{{{({r^2} +
{l^2})}^{1/2}}}} \\
= \dfrac{1}{{4\pi \varepsilon o}}\dfrac{{2ql}}{{{{({r^2} + {l^2})}^{3/2}}}} \\
$
If the dipole is infinitesimal and point P is far away then $ {l^2} $can be neglected as compared to $ {r^2} $
So,
$ E = \dfrac{1}{{4\pi \varepsilon o}}\dfrac{p}{{{r^3}}} $, parallel to $ \overrightarrow {BA} $

(b) Any surface over which the potential is constant is called an equipotential surface. In other words,
the potential difference between any two points on an equipotential surface is zero

Electric potential is zero at all points in the plane passing through the dipole equator.

Note: Always be careful while selecting the equipotential surfaces and always remember that
Any surface over which the potential is constant is called an equipotential surface. In other words, the potential difference between any two points on an equipotential surface is zero.