
How can a definite integral be negative?
Answer
465.6k+ views
Hint: We recall the definition of definite integral of function
Complete step-by-step answer:
We know that integral or primitive function of
The definite integral of the function
We can take an example
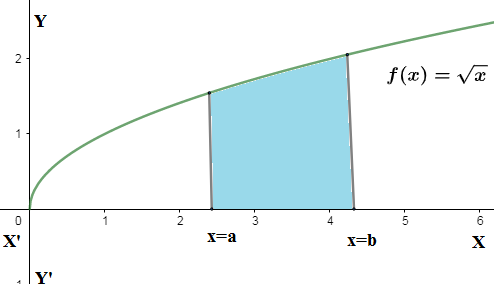
If all of the enclosed region lies blow the
We can take an example
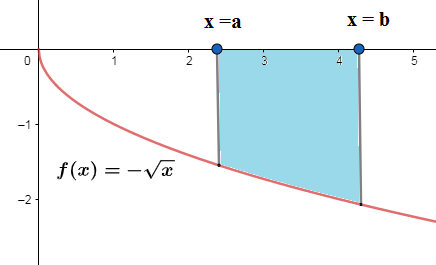
If the area of the enclosed region that lies below the
Let us consider
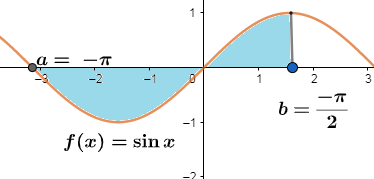
Note: We note that the definite integration of
Complete step-by-step answer:
We know that integral or primitive function of
The definite integral of the function
We can take an example

If all of the enclosed region lies blow the
We can take an example

If the area of the enclosed region that lies below the
Let us consider
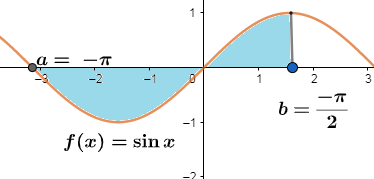
Note: We note that the definite integration of
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Draw a diagram of a flower and name the parts class 12 biology ICSE




