
A door of width of 6m has an arc above it having a height of 2m as shown. Find the radius of the arc.
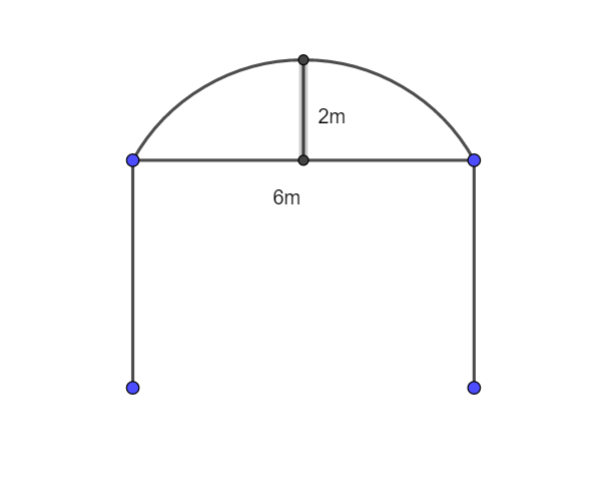

Answer
504k+ views
Hint: Assume that the radius of the circle is r. Hence determine the length OE in terms of r. Use Pythagoras theorem in triangle AOE and hence form an equation in r. Solve for r and hence determine the radius of the circular arc of the door.
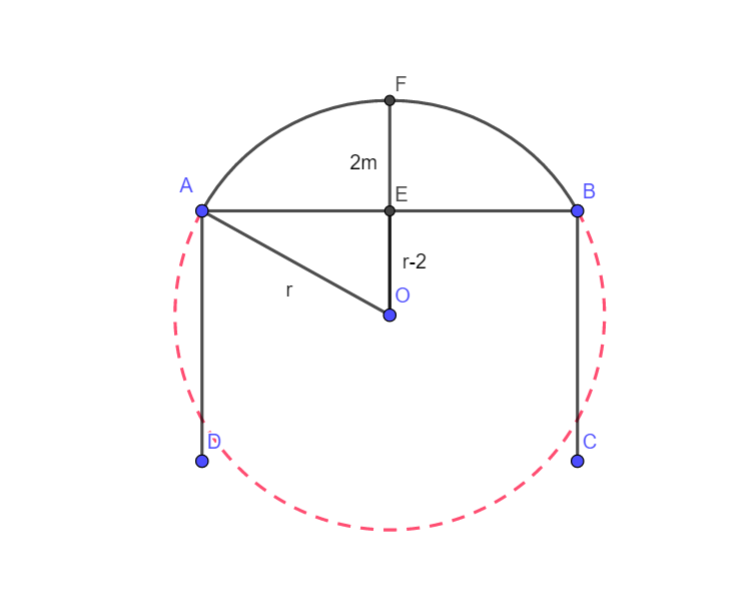
Complete step-by-step answer:
Let the radius of the circular arc of the door be r.
Hence, we have OA = OF = r.
Since FE =2 m, we have
OE = OF-FE = r-2
Also given that AB = 6m.
Since the perpendicular from the centre to the chord bisects the chord, we have AE = EB = 3m
We know that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs of the triangle. This is known as Pythagoras theorem.
Now in triangle AOE by Pythagoras theorem, we have
Substituting the values of AO, OE, and AE, we get
We know that
Hence, we have
Adding
Dividing by 4 on both sides, we get
Hence the radius of the circular arc is
Note: Alternative solution- Using sine rule and the distance of circumcentre from a side of the triangle.
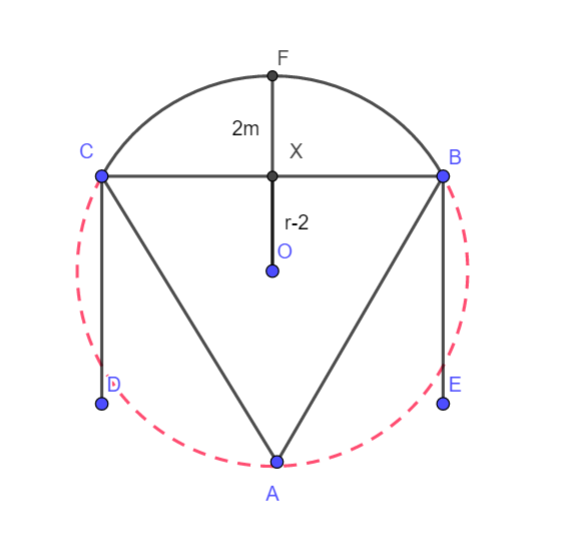
We know that the length of the side a of triangle ABC is given by
Here a = 6cm
Hence, we have
Also, we know that the distance of the circumcentre from side a is given by
Hence, we have
Squaring and adding equation (i) and (ii), we get
We know that
Hence, we have
Subtracting
Using
Hence the radius of the circle is

Complete step-by-step answer:
Let the radius of the circular arc of the door be r.
Hence, we have OA = OF = r.
Since FE =2 m, we have
OE = OF-FE = r-2
Also given that AB = 6m.
Since the perpendicular from the centre to the chord bisects the chord, we have AE = EB = 3m
We know that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs of the triangle. This is known as Pythagoras theorem.
Now in triangle AOE by Pythagoras theorem, we have
Substituting the values of AO, OE, and AE, we get
We know that
Hence, we have
Adding
Dividing by 4 on both sides, we get
Hence the radius of the circular arc is
Note: Alternative solution- Using sine rule and the distance of circumcentre from a side of the triangle.

We know that the length of the side a of triangle ABC is given by
Here a = 6cm
Hence, we have
Also, we know that the distance of the circumcentre from side a is given by
Hence, we have
Squaring and adding equation (i) and (ii), we get
We know that
Hence, we have
Subtracting
Using
Hence the radius of the circle is
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility

Difference between mass and weight class 10 physics CBSE

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE




