
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Answer
502.8k+ views
1 likes
Hint: Let us assume a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Now we let us assume the length of side AE is equal to x and length of side FD is equal to (15-x) m. Now let us draw a perpendicular from B to side AD at E. Now let us draw from a perpendicular from F to side AD at F. Let us assume the length of side BE is equal to h. So, we get the length of side CF is equal to h. Now in
Complete step-by-step answer:
From the question, we were given that a field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m.
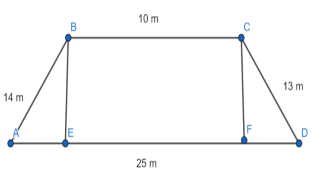
Let us assume a trapezoid whose parallel sides are equal to AD and BC whose lengths are equal to 10 m and 25 m respectively and non-parallel to equal to AB and CD is equal to 14 m and 13 m respectively. Now let us draw a perpendicular from B to side AD at E. Now let us draw from a perpendicular from F to side AD at F. Now it is clear that the length of BC is equal to EF and the length of BE is equal to CF.
Now, it is clear that
From the diagram, it is clear that the sum of length of AE, length of side EF and length of side DF is equal to length of AD.
So, it is clear that
Now by substituting equation (5) and equation (6) in equation (1).
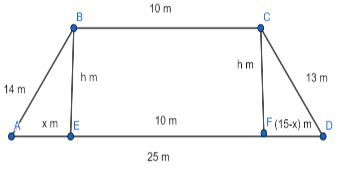
Let us assume the length of side AE is equal to x and the length of side EF is equal to 15-x.
Let us assume the length of BE is equal to h m.
So, now we should update the diagram of trapezium.
As
As
Now by using equation (9) and equation (10), and subtracting, we get
So, the length of side AE is equal to
Now we will substitute equation (11) in equation (9), we get
We know that the area of trapezium whose parallel sides are equal to a and b respectively and height of trapezium is equal to h is equal to
So, let us assume the area of trapezium whose parallel sides are equal to 10 m and 25 m and its height is equal to
So, the area of the trapezium field is equal to
Note: Students may be confused as to why it was considered that the length of BE and length of CF are equal. As AD and BC are parallel, we get the length of BC and length of EF are equal. As BE and CF are perpendicular to both AD and BC, we can say that AD and BC are parallel. We know that the distance between two parallel lines are equal. So, it is clear that the length of AD and BC are equal. This concept should be clear to the student to solve this problem.
Complete step-by-step answer:
From the question, we were given that a field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m.

Let us assume a trapezoid whose parallel sides are equal to AD and BC whose lengths are equal to 10 m and 25 m respectively and non-parallel to equal to AB and CD is equal to 14 m and 13 m respectively. Now let us draw a perpendicular from B to side AD at E. Now let us draw from a perpendicular from F to side AD at F. Now it is clear that the length of BC is equal to EF and the length of BE is equal to CF.
Now, it is clear that
From the diagram, it is clear that the sum of length of AE, length of side EF and length of side DF is equal to length of AD.
So, it is clear that
Now by substituting equation (5) and equation (6) in equation (1).
Let us assume the length of side AE is equal to x and the length of side EF is equal to 15-x.
Let us assume the length of BE is equal to h m.
So, now we should update the diagram of trapezium.

As
As
Now by using equation (9) and equation (10), and subtracting, we get
So, the length of side AE is equal to
Now we will substitute equation (11) in equation (9), we get
We know that the area of trapezium whose parallel sides are equal to a and b respectively and height of trapezium is equal to h is equal to
So, let us assume the area of trapezium whose parallel sides are equal to 10 m and 25 m and its height is equal to
So, the area of the trapezium field is equal to
Note: Students may be confused as to why it was considered that the length of BE and length of CF are equal. As AD and BC are parallel, we get the length of BC and length of EF are equal. As BE and CF are perpendicular to both AD and BC, we can say that AD and BC are parallel. We know that the distance between two parallel lines are equal. So, it is clear that the length of AD and BC are equal. This concept should be clear to the student to solve this problem.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




