
A flooring tile has the shape of a parallelogram whose base is 24 cm and its corresponding height is 10 cm. How many such tiles are required to fill a floor of area
Answer
498k+ views
Hint: The total area to be filled will be equal to the area of a single tile multiplied by the total number of tiles required. Each tile is of the shape of a parallelogram whose dimensions are given. Area of a parallelogram is the product of its height and base. Use appropriate conversion of units (1m=100cm).
Complete step-by-step answer:
We are given, total area of the floor
Since the area of the floor and dimensions of a single tile are given in different units, we need a conversion to make all the quantities to the same unit.
Therefore, total area of the floor
We are to find the number of tiles required to cover this area.
The dimensions of the tiles are given. A single tile is in the shape of a parallelogram with the length of its base as 24cm and its height as 10cm.
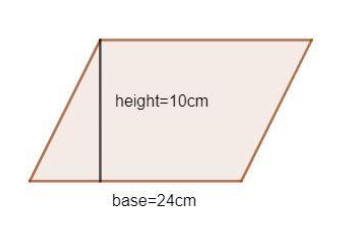
We know that,
Area of a parallelogram = Height
=
To find the number of tiles required to cover the floor we have to divide the total area of the floor by the area of a single tile.
=
=
Hence the number of tiles required to cover the floor is 45000.
Note: Key point used is that the total area to be filled will be equal to the area of single tile multiplied by the total number of tiles. Once we find the area of the parallelogram shaped tile using the established formula, we only need to do a basic division. One has to be careful to keep every quantity in the same unit while doing calculation. One also has to note that the number of tiles is a unit-less quantity.
Complete step-by-step answer:
We are given, total area of the floor
Since the area of the floor and dimensions of a single tile are given in different units, we need a conversion to make all the quantities to the same unit.
Therefore, total area of the floor
We are to find the number of tiles required to cover this area.
The dimensions of the tiles are given. A single tile is in the shape of a parallelogram with the length of its base as 24cm and its height as 10cm.

We know that,
Area of a parallelogram = Height
=
To find the number of tiles required to cover the floor we have to divide the total area of the floor by the area of a single tile.
=
=
Hence the number of tiles required to cover the floor is 45000.
Note: Key point used is that the total area to be filled will be equal to the area of single tile multiplied by the total number of tiles. Once we find the area of the parallelogram shaped tile using the established formula, we only need to do a basic division. One has to be careful to keep every quantity in the same unit while doing calculation. One also has to note that the number of tiles is a unit-less quantity.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




