Question

A glass prism has a refractive index $1.5$ and the refractive angle is $90^\circ$. If a ray falls on it at an angle of incidence of $30^\circ$, then angle of emergence will be
$\begin{align}
  & \text{A}\text{. }{{60}^{\circ }} \\
 & \text{B}\text{. 3}{{0}^{\circ }} \\
 & \text{C}\text{. 4}{{\text{5}}^{\circ }} \\
 & \text{D}\text{. The ray will not emerge out of this prism} \\
\end{align}$

Answer 1

Hint: First draw a rough figure of the condition given in the question, then apply the Snell’s law formula for incident ray, to find the value of the refracted angle. Then using the relation ${{r}_{1}}+{{r}_{2}}={{90}^{\circ }}$ find the other refracted angle. Then using the formula given by: Snell’s law for ray emerging from prism from the second refracting surface finds the angle required for total internal reflection at the second refracting surface.

Formula used:
Snell’s law for refraction states that when a ray of light travels from one medium, say medium 1, to a different medium, say medium 2 then,
${{\mu }_{1}}\sin {{\theta }_{1}}={{\mu }_{2}}\sin {{\theta }_{2}}\text{ }\cdots \cdots \left( 1 \right)$
Where
${{\mu }_{1}}$ Is the refractive index of the medium 1.
${{\theta }_{1}}$ Is the angle of incidence.
${{\mu }_{2}}$Is the refractive index of medium 2.
${{\theta }_{2}}$ Is the angle of refraction.

Complete step-by-step answer:
Let the ray incidents at an angle of ${{i}_{1}}$on the prism and emerge out at an angle ${{i}_{2}}$from the prism. The refracted angles are ${{r}_{1}}$and ${{r}_{2}}$.

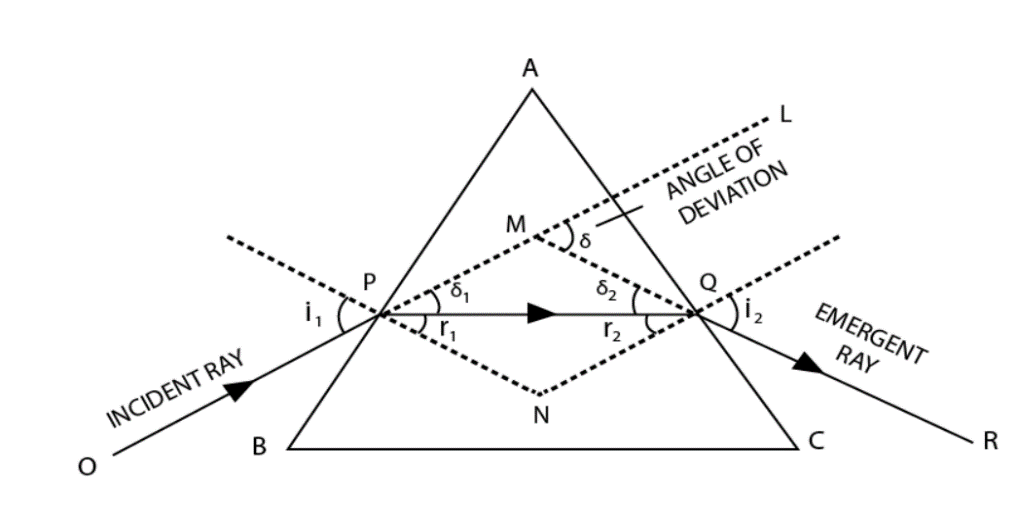
Now, using Snell’s law for incident ray or first refraction through prism. And assuming the ray incidents from air on the prism of refractive index $\mu =1.5$. So, from $E{{q}^{n}}.\to \left( 1 \right)$,
$\begin{align}
  & 1\times \sin {{30}^{\circ }}=1.5\times \sin {{r}_{1}}\text{ }\left( \because {{\mu }_{1}}=1,{{\mu }_{2}}=1.5,{{\theta }_{1}}={{i}_{1}}={{30}^{\circ }},{{\theta }_{2}}={{r}_{1}} \right) \\
 & \Rightarrow {{r}_{1}}={{\sin }^{-1}}\left( \dfrac{1}{3} \right)\text{ }\cdots \cdots \cdots \text{E}{{\text{q}}^{n}}.\to \left( 2 \right) \\
\end{align}$
Also, from triangle PNQ and quadrilateral APNQ, we have$\begin{align}
  & {{r}_{1}}+{{r}_{2}}+\theta ={{90}^{\circ }}+\theta =18{{0}^{\circ }}\text{ }\left( \angle PAQ=\text{ Angle of prism = }{{90}^{\circ }},\text{ let }\angle \text{PNQ=}\theta \right) \\
 & \Rightarrow {{r}_{1}}+{{r}_{2}}={{90}^{\circ }}\text{ }\cdots \cdots E{{q}^{n}}.\to \left( 3 \right) \\
\end{align}$
Now, substituting the value of ${{r}_{1}}$ from $E{{q}^{n}}.\to \left( 2 \right)$ in $E{{q}^{n}}.\to \left( 3 \right)$, we get
${{r}_{2}}=90-{{\sin }^{-1}}\left( \dfrac{1}{3} \right)={{70.53}^{\circ }}$
So, using Snell’s law for ray emerging from prism from second refracting surface, angle required for total internal reflection at second refracting surface is given by
$r={{\sin }^{-1}}\left( \dfrac{1}{\mu } \right)={{\sin }^{-1}}\left( \dfrac{1}{1.5} \right)={{41.81}^{\circ }}\text{ }\left( \because \mu \text{ is refractive index of prism} \right)$
Since $\mu $ is the refractive index of the prism.
Since, the value of ${{r}_{2}}$ is greater than the value of $r$, so the ray will not emerge out of the prism and will get internally reflected.
Hence, the correct answer is (d).

Additional Information:
A prism is a homogenous, transparent medium enclosed by two plane surfaces inclined at an angle. These surfaces are called the ‘refracting surfaces’. The angle between these refractive surfaces is called the ‘angle of prism’. Rays incident on one refracting surface and come out of another. The angle at which the rays strike the refracting surface is called incident angle and the angle at which they emerge out of prism through another refracting surface is called the angle of emergence.

Note: When a ray of light travels from denser medium to rarer medium there is a chance that total internal reflection may occur if angle of incidence is greater than the angle required for total internal reflection. So, one should check for it while dealing with such types of problems.