Question

A heap of rice is in the form of a cone of diameter \[9\;m\] and height \[3.5\;m\] . The volume of the rice is \[74.25\;{m^3}\] approximately. Canvas cloth required to just cover the heap is \[80.62\;{m^2}\] approximately. Write 1 if true and 0 if false.

Answer 1

Hint: Given that the cone is in the form of heap and so it must be a right-circular cone. Also, given that the diameter of the cone with which we shall find the radius of the cone which is half of the diameter. Use the formula for volume of a right-circular cone to find the volume of the given cone. Canvas cloth required to just cover the heap is the same as the value of the lateral surface area of the cone which can be arrived at using the formula for lateral surface area of the right-circular cone.

Complete step-by-step answer:
Given that the diameter of the cone is \[9\;m\] .
We know that the base radius of the cone is equal to half of the diameter of that cone.
Let \[R = \] Base radius of the given cone, \[D = \] Diameter of the given cone and \[H = \] Height of the given cone.

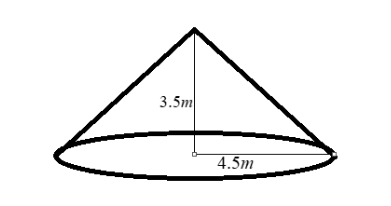
We have that \[R = \dfrac{1}{2}D = \dfrac{1}{2}\left( 9 \right) = 4.5\;m\] and \[H = 3.5\;m\] .
Given that the cone is in the form of a heap and so it must be a right-circular cone.
We know that the formula for the volume of a right-circular cone is \[\dfrac{1}{3}\pi {R^2}H\] .
Then, the volume of the given heap of rice in the form of a right-circular
\[ = \dfrac{1}{3} \times {\left( {4.5} \right)^2} \times 3.5\pi = \dfrac{1}{3} \times 20.25 \times 3.5\pi = 23.625\pi \simeq 74.25\;{m^3}\]
Observe that Canvas cloth required to just cover the heap is the same as the value of the lateral surface area of the cone.
The formula for the lateral surface area of the right-circular cone is \[\pi R\left( {\sqrt {{R^2} + {H^2}} } \right)\]
The lateral surface area of the given cone
\[ = 4.5\left( {\sqrt {{{4.5}^2} + {{3.5}^2}} } \right)\pi = 4.5\left( {\sqrt {20.25 + 12.25} } \right)\pi = 4.5\left( {\sqrt {32.5} } \right)\pi \simeq 80.6266 \simeq 80.62\;{m^2}\]
Canvas cloth required to just cover the heap \[ \simeq 80.62\;{m^2}\] .
Therefore, the given statement is true. The answer is 1.
So, the correct answer is “1”.

Note: Here we considered the value of \[\pi \] to be \[\dfrac{{22}}{7}\] . We shall also consider the value of \[\pi \] to be \[3.14\] which is an approximate value. Since \[\pi \] is an irrational number it’s exact value can never be calculated. So, we have only arrived at an approximate solution to the given problem.