Questions & Answers
Question
AnswersA heap of wheat is in the form of a cone whose diameter is 10.5m and the height is 3m.Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of canvas required.
Answer
Verified149.4k+ views
Hint- The heap is enclosed as a conic section which is cone in this case. Volume of heap can easily be calculated using the direct formula of volume of cone. The area of the canvas required to protect the heap will be the curved surface area of the cone.
The diameter of the cone, D=10.5m thus
Radius of cone, r = $\dfrac{D}{2} = \dfrac{{10.5}}{2} = 5.25m$
Height of cone, H = 3m
The volume of cones is given as $\dfrac{1}{3}\pi {r^2}H$…………………………. (1)
Putting the values in equation (1)
Volume = $\dfrac{1}{3}\pi \times {5.25^2} \times 3$
$ \Rightarrow $ Volume = $\left( {\dfrac{1}{3} \times \dfrac{{22}}{7} \times 82.68} \right)$
$ \Rightarrow $ Volume = 86.625 ${m^3}$
Now the heap is covered by a canvas to protect it from rain, thus the area of the canvas that we will be using for the conic section (cone) will be the curved surface area of that conic section.
Curved surface area of the cone is $\pi rl$ where r is radius and l is the slant height……………. (2)
Now slant height can be calculated using Pythagoras theorem which is $hypotenu{s^2} = perpendicula{r^2} + bas{e^2}$
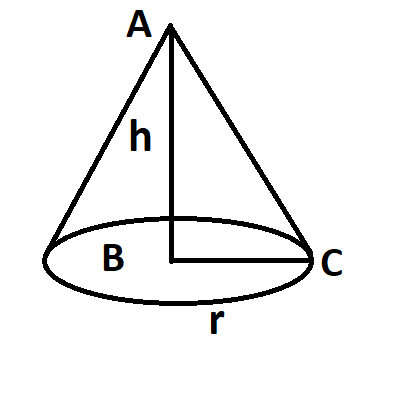
In triangle ABC
$A{C^2} = A{B^2} + B{C^2}$…………………… (3)
Now AC = l (slant height), BC= r (radius of base), AB = h (height)
So using the above figure ${l^2} = {h^2} + {r^2}$
Putting the values we get
$ \Rightarrow {l^2} = {3^2} + {\left( {5.25} \right)^2}$
Hence ${l^2} = 9 + 27.5625 = 36.5625$
Hence l=6.0467 m
Now using equation (2)
Curved surface area = $\pi rl$
$ \Rightarrow $Curved surface area = $\dfrac{{22}}{7} \times 5.25 \times 6.0467$
On solving curved surface area = 99.77 ${m^2}$
Note – Whenever we face such problems the key concept that we need to recall that whenever being asked about the area associated with a cone, then always we have to find the curved surface area. Another note point is the height, radius of base and the slant height of a cone forms a right angle triangle.
The diameter of the cone, D=10.5m thus
Radius of cone, r = $\dfrac{D}{2} = \dfrac{{10.5}}{2} = 5.25m$
Height of cone, H = 3m
The volume of cones is given as $\dfrac{1}{3}\pi {r^2}H$…………………………. (1)
Putting the values in equation (1)
Volume = $\dfrac{1}{3}\pi \times {5.25^2} \times 3$
$ \Rightarrow $ Volume = $\left( {\dfrac{1}{3} \times \dfrac{{22}}{7} \times 82.68} \right)$
$ \Rightarrow $ Volume = 86.625 ${m^3}$
Now the heap is covered by a canvas to protect it from rain, thus the area of the canvas that we will be using for the conic section (cone) will be the curved surface area of that conic section.
Curved surface area of the cone is $\pi rl$ where r is radius and l is the slant height……………. (2)
Now slant height can be calculated using Pythagoras theorem which is $hypotenu{s^2} = perpendicula{r^2} + bas{e^2}$
In triangle ABC
$A{C^2} = A{B^2} + B{C^2}$…………………… (3)
Now AC = l (slant height), BC= r (radius of base), AB = h (height)
So using the above figure ${l^2} = {h^2} + {r^2}$
Putting the values we get
$ \Rightarrow {l^2} = {3^2} + {\left( {5.25} \right)^2}$
Hence ${l^2} = 9 + 27.5625 = 36.5625$
Hence l=6.0467 m
Now using equation (2)
Curved surface area = $\pi rl$
$ \Rightarrow $Curved surface area = $\dfrac{{22}}{7} \times 5.25 \times 6.0467$
On solving curved surface area = 99.77 ${m^2}$
Note – Whenever we face such problems the key concept that we need to recall that whenever being asked about the area associated with a cone, then always we have to find the curved surface area. Another note point is the height, radius of base and the slant height of a cone forms a right angle triangle.