
A hollow square shaped tube open at both ends is made of iron. The side of the internal square is
Answer
472.8k+ views
2 likes
Hint: Firstly check the side length of the external square and then the volume of the external square and equate it to the given volume of the tube and find the thickness of the tube.
Complete step-by-step answer:
A hollow square shaped tube open at both ends is made of iron. The side of the internal square is
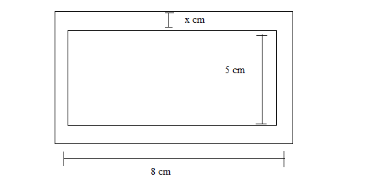
Let us assume that the thickness of the tube is equal to
As per given the side of the internal square is
As given that the length of the tube is equal to
So, the volume of the square is equal to
The volume of the internal square is equal to
Now as per given there is
Further simplify,
Hence, the thickness of the tube is equal to
So, the correct answer is “
Note: Please make the diagram of the tube to avoid any confusion for the side length of the tube and of internal and external squares. Also use the formula for the volume of the cuboid as the product of length to breadth to height.
Complete step-by-step answer:
A hollow square shaped tube open at both ends is made of iron. The side of the internal square is

Let us assume that the thickness of the tube is equal to
As per given the side of the internal square is
As given that the length of the tube is equal to
So, the volume of the square is equal to
The volume of the internal square is equal to
Now as per given there is
Further simplify,
Hence, the thickness of the tube is equal to
So, the correct answer is “
Note: Please make the diagram of the tube to avoid any confusion for the side length of the tube and of internal and external squares. Also use the formula for the volume of the cuboid as the product of length to breadth to height.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE




