Question

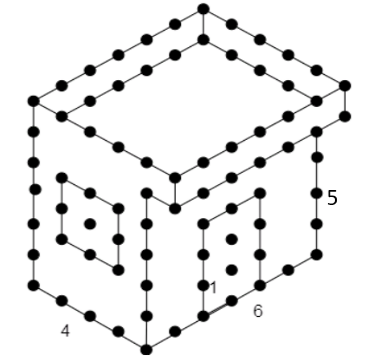
A house design given on an isometric dot sheet in an adjacent figure. Measure the length, breadth, and height of the house. The slab is projected forward. Find the area of the slab.

Answer 1

Hint: In this question, we need to observe the given figure carefully to get the values of length, height, and breadth of the given house design. Now, from the figure, we can notice that the slab is extended by one unit forward which further gives the values of length and breadth of the slab. Then substitute these values in the area of the rectangle formula which is given by \[A=l\times b\] to get the area of the slab.

Complete step-by-step solution -
CUBOID: Any figure which is surrounded by six rectangular surfaces is called a cuboid.
The three dimensions of the cuboid are length, breadth, and height
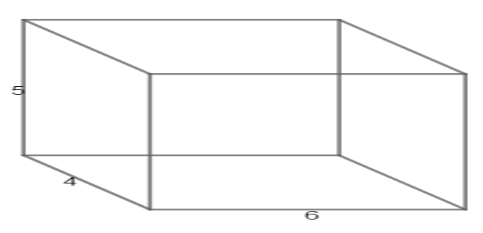
Now, from the given figure in the question, we can find that the design of the house is in the form of a cuboid.
Let us now calculate its dimensions length, breadth, and height from the given figure.
As we already know that the distance between two adjacent points in an isometric sheet is given by 1 unit.

Now, on counting the dots in the respective directions we get the dimensions of the given design as
\[\text{length}=6\]
\[\text{breadth}=4\]
\[\text{height}=5\]
Now, from the figure, we can observe that the slab is projected 1 unit forward
Now, the breadth of the slab increases by one unit than that of the cuboid
Let us assume the length of the slab as l and breadth as b and area as A
As we already know that the slab is in the form of a rectangle whose area can be calculated from the formula
\[\Rightarrow A=l\times b\]

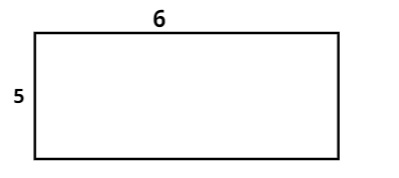
Now, we get the values of dimensions of the slab as
\[l=6,b=5\]
Now, on substituting the respective values in the formula we get,
\[\Rightarrow A=6\times 5\]
Now, on further simplification we get,
\[\therefore A=30\]
Hence, the area of the slab in the design is 30 units.

Note: It is important to note that adjacent points have unit distance as it is an isometric sheet. While measuring the dimensions we should not neglect any of the points and need to note the dimensions accordingly as length, breadth, and height. It is also to be noted that the breadth of the slab is getting increased by 1 unit but not the length. Because considering it in the other way changes the complete result.