Question

A line lies in the xy-plane and makes an angle of \[{30^ \circ }\] with the positive x- axis. Find its direction cosines.

Answer 1

Hint: We will first see the angle it is making with all of the axis that is x-axis, y-axis and z-axis. Then, by finding the cosines of all of those angles, we will get the direction cosines of the line.

Complete step-by-step answer:
Let us first draw the plane and the line as given in the question.

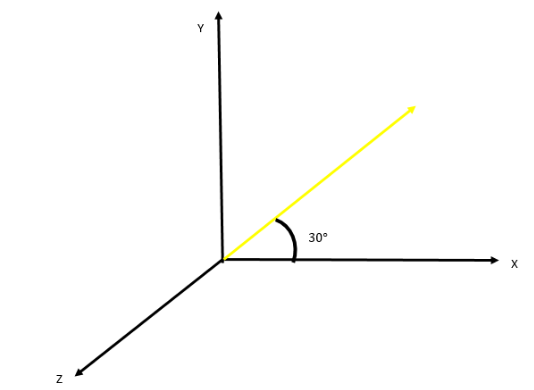
Here, the yellow line is the line which is in the xy-plane making an angle of \[{30^ \circ }\] with the positive x- axis.
We see that we are already given the angle it makes with the x – axis. Now, we just need to find its angle from y – axis and z – axis.
Now, we know that x – axis and y – axis are perpendicular to each other. Hence, the angle which the yellow line makes with y – axis will be complimentary. Hence, the angle will be ${90^ \circ } - {30^ \circ } = {60^ \circ }$.
Hence, the yellow line is making an angle of ${60^ \circ }$ with y – axis.
Now, we know that the xy – plane will be perpendicular to the z – axis.${90^ \circ }$ Hence, it will make an angle with the z – axis.
Now, the direction cosines are the cosine of all the angles.
Therefore it will be $(\cos {30^ \circ },\cos {60^ \circ },\cos {90^ \circ })$.
Putting its values, we will get:-
Direction cosines are $\left( {\dfrac{{\sqrt 3 }}{2},\dfrac{1}{2},0} \right)$.
Hence, the answer is $\left( {\dfrac{{\sqrt 3 }}{2},\dfrac{1}{2},0} \right)$.

Additional Information: Direction cosines are useful for forming direction cosine matrices that express one set of orthonormal basis vectors in terms of another set, or for expressing a known vector in a different basis. The name of direction cosines itself has the word cosines in it. You may remember it by that way as well. You just have to find the cosines of all the angles which the line makes with all the axes in coordinate axes.

Note: The students must make the diagram for the clarity of things.
You must note that all the planes like the xy – plane and so on are perpendicular to the left axis that is the z – axis and similarly with all the other axes.