Question

A magnet with its north pole pointing downwards along the axis of an open ring is as illustrated. As the magnet reaches close to the centre of the ring,

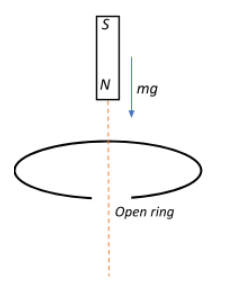
A.Its acceleration becomes greater than g
B.Its acceleration becomes less than g
C.Its acceleration remains equal to g
D.None of the above

Answer 1

Hint: Recall that a change in magnetic flux induces a current. Now, an induced current would produce an induced magnetic field that would oppose the path of the magnet’s magnetic field. If that is the case, given that this is an open ring, we know that an emf will be induced, but will a current be induced? Also, remember that the magnet is falling under the influence of a gravitational force. So in any case the acceleration experienced by a magnet will include the one due to gravity, if not anything else.

Complete answer:
We can understand the context of this scenario by bringing in Faraday’s First Law of Electromagnetism.
Faraday’s first law suggests that whenever the magnetic flux linked with a coil changes, an emf is induced in the coil. The induced emf exists as long as the change in magnetic flux continues to exist. Recall that magnetic flux here is nothing but the magnetic field lines emanating from the magnet.
In the scenario presented to us, the change in the magnetic flux is brought about by the magnet moving towards the ring. The intensity of the magnetic field, and hence the magnetic flux increases as the magnet approaches the plane of the ring.
Using Faraday’s first law we can say that this change in flux introduces an emf or a potential difference across the ends of the ring. This potential difference would usually induce a current that would flow around the ring, but since this is an open ring (equivalent to an open circuit), there is no induced current flowing through it.
This lack of induced current implies that there is no induced magnetic field that opposes the magnet’s magnetic field, and hence the motion of the magnet faces zero opposition from the ring. (Lenz’s law).
This means that the only force contributing to the motion of the magnet through the ring is the gravitational force that is pulling the magnet downwards by its weight. The acceleration that the magnet experiences is thus solely due to the acceleration due to gravity, since gravitational force is the only influencing force in this system. Thus, the magnet falls with an acceleration $a=g$ since the net force acting on the magnet is $F_{net} = mg$.

Thus, the correct choice would be C. Its acceleration remains equal to g.

Note:
Remember that if the ring was closed, our inferences would be entirely different. When the magnet approaches the ring, the variation in flux induces an emf which in turn induces a current that flows in a direction such that it opposes the approach of the magnet. Thus, the acceleration of the magnet decreases and becomes a < g. After passing through the ring, there is a decrease in flux linked with the ring which produces an emf in the ring and the current thus induced will have a direction such that it opposes the recession of the magnet from the ring. This impedes the acceleration of the magnet and is still a < g.