Question

A man \[160cm\] tall, walks away from a source of light situated at the top of a pole \[6m\] high, at the rate of \[1.1m/{\mathop{\rm s}\nolimits} \]. How fast is the length of his shadow increasing when he is \[1m\] away from the pole?

Answer 1

Hint: In the given question, we have been given that there is a \[160cm\] or \[1.6m\] tall man. Then there is a light which is situated at the top of a pole which is \[6m\] in height. The man is traveling away from the pole at the speed of \[1.1m/{\mathop{\rm s}\nolimits} \]. We have to calculate the rate at which his shadow is increasing when he is \[1m\] away from the pole. For solving the question, we are going to first draw the position of the man and the light and try to form a recognizable shape from it. Then we are going to apply some basic concepts on it so as to calculate the answer of the same.

Formula Used:
In the given question, we are going to use the formula of differentiation, which is:
\[\dfrac{{d\left( {{x^n}} \right)}}{{dx}} = n{x^{n - 1}}\]

Complete step-by-step answer:
First, let us draw the position of the man and the light. And we are going to have a triangle after doing that. And let us name them as shown.

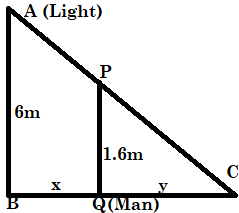
Now, C is the point where his shadow falls.
Clearly, \[\Delta ABC\] and \[\Delta PQC\] are similar.
Hence, \[\dfrac{{AB}}{{BC}} = \dfrac{{PQ}}{{QC}}\]
Putting in values,
\[\dfrac{6}{{x + y}} = \dfrac{{1.6}}{y}\]
Cross multiplying,
$\Rightarrow$ \[6y = 1.6x + 1.6y\]
Taking the like terms to one side,
$\Rightarrow$ \[6y - 1.6y = 1.6x\]
$\Rightarrow$ \[4.4y = 1.6x\]
Solving for \[y\],
\[y = \dfrac{{1.6}}{{4.4}}x = \dfrac{4}{{11}}x\] …(i)
Now, for the rate of change of shadow, we want \[\dfrac{{dy}}{{dt}}\]
So, differentiating (i) with respect to \[t\], we have
$\Rightarrow$ \[\dfrac{{dy}}{{dt}} = \dfrac{4}{{11}} \times \dfrac{{dx}}{{dt}}\]
Now, the speed of man is \[1.1m/s\], hence, \[\dfrac{{dx}}{{dt}} = 1.1\]
Thus, \[\dfrac{{dy}}{{dt}} = \dfrac{4}{{11}} \times 1.1 = 0.4m/s\]
So, the length of the shadow is moving at the pace of \[0.4m/s\] and is independent of the man's position from the light.
Note: So, for solving questions of such type, we first write what has been given to us. Then we write down what we have to find. Then we think about the formulae which contain the known and the unknown and pick the one which is the most suitable and the most effective for finding the answer of the given question. Then we put in the knowns into the formula, evaluate the answer and find the unknown. It is really important to follow all the steps of the formula to solve the given expression very carefully and in the correct order, because even a slightest error is going to make the whole expression awry and is going to give us an incorrect answer.