
A man is standing on a weighing machine placed in a lift, when stationary, his weight is recorded as 40 kg. If the lift is accelerated upwards with an acceleration of \[2\,m/{s^2}\], then the weight recorded in the machine will be
A. 48 kg
B. 32 kg
C. 64 kg
D. 80 kg
Answer
568.8k+ views
Hint: Draw the free body diagram of the forces acting on the man in the accelerated lift. The normal reaction provided by the floor of the lift determines the weight of the man. If the normal reaction changes, the weight of the man also changes.
Formula used:
Weight of the body of mass m is,
\[W = mg\]
Here, g is the acceleration due to gravity.
Complete step by step answer:
We have given the weight of the man in a lift when it is stationary. While the man was stationary, the normal force provided by the base of the lift is equal to the weight of the man. We know that the normal force provided by the ground determines the weight of the body.
Now, when the lift accelerates upwards with acceleration \[2\,m/{s^2}\], we can draw the free body diagram of the forces acting on the man as shown in the figure below.
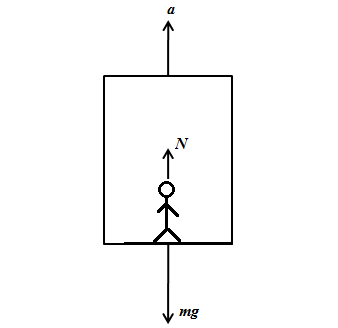
Now, we apply Newton’s second law of motion in the vertical direction of motion as follows,
\[N - mg = ma\]
\[ \Rightarrow N = m\left( {a + g} \right)\]
Here, N is the normal force, m is the mass of the man, g is the acceleration due to gravity and a is the uniform acceleration of the lift.
Substituting 40 kg for m, \[10\,m/{s^2}\] for g and \[2\,m/{s^2}\] for a in the above equation, we get,
\[N = \left( {40} \right)\left( {2 + 10} \right)\]
\[ \Rightarrow N = 480\,{\text{N}}\]
This is of course the weight of the man while in the accelerated lift. We know that,
\[W = mg\]
\[ \Rightarrow m = \dfrac{W}{g}\]
Substituting 480 N for W and \[10\,m/{s^2}\] for g in the above equation, we get,
\[m = \dfrac{{480}}{{10}}\]
\[ \Rightarrow m = 48\,kg\]
Therefore, the weight of the man in the lift will be 48 kg.
So, the correct answer is “Option A”.
Note:
The weighing machine measures the mass of the body and not the weight. We know that the mass of the body always remains constant whether you are on the earth or on the outer planet. The quantity which varies from place to place, planet to planet is the weight of the body due to different values of acceleration due to gravity. The weighing machine shows change in the mass of the man because the value of acceleration due to gravity is fixed for the machine.
Formula used:
Weight of the body of mass m is,
\[W = mg\]
Here, g is the acceleration due to gravity.
Complete step by step answer:
We have given the weight of the man in a lift when it is stationary. While the man was stationary, the normal force provided by the base of the lift is equal to the weight of the man. We know that the normal force provided by the ground determines the weight of the body.
Now, when the lift accelerates upwards with acceleration \[2\,m/{s^2}\], we can draw the free body diagram of the forces acting on the man as shown in the figure below.

Now, we apply Newton’s second law of motion in the vertical direction of motion as follows,
\[N - mg = ma\]
\[ \Rightarrow N = m\left( {a + g} \right)\]
Here, N is the normal force, m is the mass of the man, g is the acceleration due to gravity and a is the uniform acceleration of the lift.
Substituting 40 kg for m, \[10\,m/{s^2}\] for g and \[2\,m/{s^2}\] for a in the above equation, we get,
\[N = \left( {40} \right)\left( {2 + 10} \right)\]
\[ \Rightarrow N = 480\,{\text{N}}\]
This is of course the weight of the man while in the accelerated lift. We know that,
\[W = mg\]
\[ \Rightarrow m = \dfrac{W}{g}\]
Substituting 480 N for W and \[10\,m/{s^2}\] for g in the above equation, we get,
\[m = \dfrac{{480}}{{10}}\]
\[ \Rightarrow m = 48\,kg\]
Therefore, the weight of the man in the lift will be 48 kg.
So, the correct answer is “Option A”.
Note:
The weighing machine measures the mass of the body and not the weight. We know that the mass of the body always remains constant whether you are on the earth or on the outer planet. The quantity which varies from place to place, planet to planet is the weight of the body due to different values of acceleration due to gravity. The weighing machine shows change in the mass of the man because the value of acceleration due to gravity is fixed for the machine.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




