
Answer
466.8k+ views
Hint: The medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the cylindrical part of the capsule and the diameter of the hemispheres are given. The volume of a cylinder having length h and radius r is given by $\pi {{r}^{2}}h$. Again , volume of a hemisphere with radius r is given by $\dfrac{2}{3}\pi {{r}^{3}}$ .
Find the individual volumes of the cylinder and the hemispheres using these formulae.
Now, note that the total volume of the capsule is the sum of the volumes of the cylinder and the hemispheres.
Complete step-by-step solution:
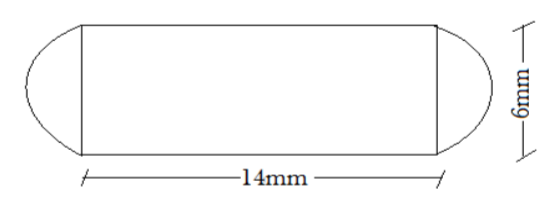
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends.
The length of the cylindrical part of the capsule is 14mm, and the diameter of hemisphere is 6mm.
Therefore the total volume of the capsule is the sum of the volumes of the cylinder and the hemispheres.
The cylindrical part of the capsule has length 14mm and radius $\dfrac{6}{2}=3$mm.
We know, the volume of a cylinder having length h and radius r is given by $\pi {{r}^{2}}h$
∴ Applying the formula we find the volume of the cylinder as $\text{ }\!\!\pi\!\!\text{ }\!\!\times\!\!\text{ (3}{{\text{)}}^{\text{2}}}\text{ }\!\!\times\!\!\text{ 14=126 }\!\!\pi\!\!\text{ =396m}{{\text{m}}^{3}}$ (taking π=22/7)
Again we know, volume of a hemisphere with radius r is given by $\dfrac{2}{3}\pi {{r}^{3}}$
The volume of each hemisphere with radius 3mm will be $\dfrac{2}{3}\pi {{\left( 3 \right)}^{3}}=\dfrac{2}{3}\times \pi \times 27=18\pi =56.52\text{m}{{\text{m}}^{3}}$ Therefore the total volume of the capsule is = volumes of the cylinder + volume of two hemispheres, i.e.
$\begin{align}
& 396+\left( 2\times 56.52 \right) \\
& =396+113.04 \\
& =509.04m{{m}^{3}} \\
\end{align}$
Hence, the volume of the medicine capsule is $509.04m{{m}^{3}}$.
Note:
Note the formulae of finding the volume of the following figures.
Find the individual volumes of the cylinder and the hemispheres using these formulae.
Now, note that the total volume of the capsule is the sum of the volumes of the cylinder and the hemispheres.
Complete step-by-step solution:

A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends.
The length of the cylindrical part of the capsule is 14mm, and the diameter of hemisphere is 6mm.
Therefore the total volume of the capsule is the sum of the volumes of the cylinder and the hemispheres.
The cylindrical part of the capsule has length 14mm and radius $\dfrac{6}{2}=3$mm.
We know, the volume of a cylinder having length h and radius r is given by $\pi {{r}^{2}}h$
∴ Applying the formula we find the volume of the cylinder as $\text{ }\!\!\pi\!\!\text{ }\!\!\times\!\!\text{ (3}{{\text{)}}^{\text{2}}}\text{ }\!\!\times\!\!\text{ 14=126 }\!\!\pi\!\!\text{ =396m}{{\text{m}}^{3}}$ (taking π=22/7)
Again we know, volume of a hemisphere with radius r is given by $\dfrac{2}{3}\pi {{r}^{3}}$
The volume of each hemisphere with radius 3mm will be $\dfrac{2}{3}\pi {{\left( 3 \right)}^{3}}=\dfrac{2}{3}\times \pi \times 27=18\pi =56.52\text{m}{{\text{m}}^{3}}$ Therefore the total volume of the capsule is = volumes of the cylinder + volume of two hemispheres, i.e.
$\begin{align}
& 396+\left( 2\times 56.52 \right) \\
& =396+113.04 \\
& =509.04m{{m}^{3}} \\
\end{align}$
Hence, the volume of the medicine capsule is $509.04m{{m}^{3}}$.
Note:
Note the formulae of finding the volume of the following figures.
| Figure | Volume |
| Cube | $a^3$ |
| Cuboid | $l\times b\times h$ |
| Sphere | $\dfrac{4}{3}\pi {{r}^{3}}$ |
| Hemisphere | $\dfrac{2}{3}\pi {{r}^{3}}$ |
| Cylinder | $\pi {{r}^{2}}h$ |
| Cone | $\dfrac{1}{3}\pi {{r}^{2}}h$ . |
Recently Updated Pages
Glycerol can be separated from spentlye in soap industry class 9 chemistry CBSE

Glycerol can be separated from spentlye in soap industry class 9 chemistry CBSE

Glycerol can be separated from spentlye in soap industry class 9 chemistry CBSE

Glycerol can be separated from spentlye in soap industry class 9 chemistry CBSE

Glycerol can be separated from spentlye in soap industry class 9 chemistry CBSE

Glycerol can be separated from spentlye in soap industry class 9 chemistry CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Voters list is known as A Ticket B Nomination form class 9 social science CBSE

The president of the constituent assembly was A Dr class 9 social science CBSE




