Question

A metallic cylinder of diameter $3$ cm and height $3\dfrac{1}{3}$ cm is melted and cast into a sphere. Find the diameter of the sphere.

Answer 1

Hint: The metallic cylinder is converted into a metallic sphere. In this conversion the volume remains the same for both the cylinder and sphere. So equate both the volumes and find the radius and then we can find diameter as twice the radius.

Complete step-by-step answer:

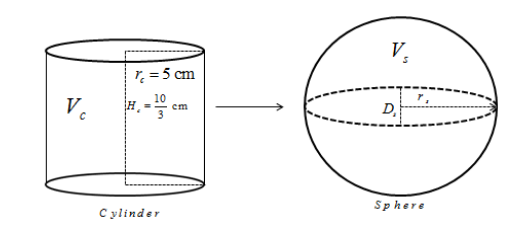
Given information
Cylinder:
Diameter of cylinder, ${D_c} = 5$ cm
Radius of the cylinder is given by,
 ${r_c} = \dfrac{D}{2}$
${r_c} = \dfrac{5}{2}$ cm
Height of the cylinder, ${H_c} = 3\dfrac{1}{3} = \dfrac{{10}}{3}$ cm
The volume of the cylinder is given by,
$V = \pi {r_c}^2{H_c} \cdots \left( 1 \right)$
Substituting the value of and in equation (1), we get
$\Rightarrow V = \pi {\left( {\dfrac{5}{2}} \right)^2}\left( {\dfrac{{10}}{3}} \right) \cdots \left( 2 \right)$
Sphere
Let the radius and diameter of the sphere be and respectively.
Volume of the sphere is given by,
${V_s} = \dfrac{4}{3}\pi {r_s}^3 \cdots \left( 3 \right)$
According to the question the metallic cylinder is converted into a metallic sphere. In this process of conversion the volume of the cylinder will be the same as that of the sphere.
Therefore, equating (2) and equation (3) , we get
$\Rightarrow \pi {\left( {\dfrac{5}{2}} \right)^2}\left( {\dfrac{{10}}{3}} \right) = \dfrac{4}{3}\pi {r_s}^3$
Cancelling the $\pi $ from both sides,
$\Rightarrow \left( {\dfrac{{25}}{4}} \right)\left( {\dfrac{{10}}{3}} \right) = \dfrac{4}{3}{r_s}^3$
There is only one variable in this equation and i.e. ${r_s}$ . Solving for ${r_s}$ we get,
$
\Rightarrow \left( {\dfrac{{25}}{4}} \right)\left( {\dfrac{{10}}{3}} \right) = \dfrac{4}{3}{r_s}^3 \\
\Rightarrow {r_s}^3 = \dfrac{{25 \times 10 \times 3}}{{4 \times 3 \times 4}} \\
\Rightarrow {r_s}^3 = \dfrac{{125}}{8} \\
\Rightarrow {r_s} = \sqrt[3]{{\dfrac{{125}}{8}}} \\
\Rightarrow {r_s} = 2.5{\text{ cm}} \\
 $
The diameter of the sphere is twice its radius.
$
\Rightarrow {D_s} = 2{r_s} \\
\Rightarrow {D_s} = 2\left( {2.5} \right) \\
\Rightarrow {D_s} = 5{\text{ cm}} \\
 $
Hence, the diameter of the sphere is, ${D_s} = 5{\text{ cm}}$.

Note: In problems of these types where one shape is converted into another shape, the concept of constant volume should be applied.
For instance, if the cone of radius ${r_c}$ and height ${h_c}$ is converted into a sphere of radius ${r_s}$ . then also the concept of constant volume is used as
Volume of cone = Volume of Sphere.
$\dfrac{1}{3}\pi {r_c}^2{h_c} = \dfrac{4}{3}\pi {r_s}^3$
The only unknown in this equation (i) is ${r_s}$ .So it can be solved for ${r_s}$.