Question

A metallic disc, in the shape of a right circular cylinder, is of height 2.5 mm and base radius 12 cm. Metallic disc is melted and made into a sphere. Calculate the radius of the sphere.

Answer 1

Hint: In this question, we first need to find the volume of the metallic using the formula of volume of a right cylinder given by \[\pi {{r}^{2}}h\]. Then equate this volume to the volume of the sphere which is given by the formula \[\dfrac{4}{3}\pi {{r}^{3}}\]. Now, on further simplification gives the radius of the sphere
Complete step by step answer:
RIGHT CIRCULAR CYLINDER:
A right circular cylinder is considered as a solid generated by the revolution of a rectangle about one of its sides.
Volume of a right circular cylinder is given by the formula
\[\pi {{r}^{2}}h\]
SPHERE:
A sphere is a solid generated by the revolution of a semicircle about its diameter.
Volume of a sphere is given by the formula
\[\dfrac{4}{3}\pi {{r}^{3}}\]
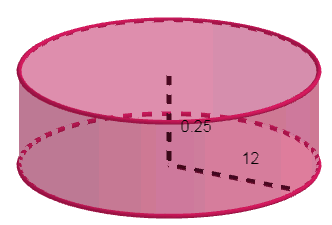
Now, given in the question that metallic disc is in the form a right circular cylinder with
\[r=12cm,h=2.5mm\]
Now, let us convert the height into cm
\[r=12cm,h=0.25cm\]

Now, let us find the volume of the metallic disc
\[\Rightarrow \pi {{r}^{2}}h\]
Now, on substituting the respective values we get,
\[\Rightarrow \pi \times {{12}^{2}}\times 0.25\]
Now, on further simplification we get,
\[\Rightarrow 36\pi \]
Now, let us assume the radius of the sphere as r

Let us now find the volume of the sphere which is given by
\[\Rightarrow \dfrac{4}{3}\pi {{r}^{3}}\]
Now, on equating this volume with the volume of the metallic disc we get,
\[\Rightarrow \dfrac{4}{3}\pi {{r}^{3}}=36\pi \]
Now, on cancelling the common terms on both sides we get,
\[\Rightarrow \dfrac{4}{3}{{r}^{3}}=36\]
Now, on rearranging the terms and simplifying further we get,
\[\Rightarrow {{r}^{3}}=9\times 3\]
Now, this can be further written as
\[\Rightarrow {{r}^{3}}={{3}^{3}}\]
Now, on further simplification we get,
\[\therefore r=3cm\]

Note:
It is important to note that as we are melting the metallic disc to sphere here the volume remains unchanged so on equating them correspondingly we get the radius sphere.
Instead of considering the volume to be unchanged if we consider that the area remains the same then the result so obtained will be incorrect. Also, we need to substitute the respective values while simplifying.