
A parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers $\dfrac{1}{3}$ of the area of its plates, as shown in the figure. The total capacitance is C while that of the portion with dielectric in between is \[{{C}_{1}}\]. When the capacitor is charged, the plate area covered by the dielectric gets charged ${{Q}_{1}}$ and the rest of the area gets charged ${{Q}_{2}}$. The electric field in the dielectric is ${{E}_{1}}$ and that in the other portion is ${{E}_{2}}$. Choose the correct option/options, ignoring the edge effects:

$\begin{align}
& \text{A}\text{. }\dfrac{{{E}_{1}}}{{{E}_{2}}}=1 \\
& \text{B}\text{. }\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{1}{K} \\
& \text{C}\text{. }\dfrac{{{Q}_{1}}}{{{Q}_{2}}}=\dfrac{3}{K} \\
& \text{D}\text{. }\dfrac{C}{{{C}_{1}}}=\dfrac{2+K}{K} \\
\end{align}$

Answer
509.4k+ views
Hint: The capacitance of a parallel plate capacitor needs to be found in this problem. The formula of a parallel plate capacitor is given by: \[C=\dfrac{K{{\in }_{0}}A}{d}\]. For capacitors in parallel to each other, the net capacitance is given by, ${{C}_{net}}={{C}_{1}}+{{C}_{2}}$. Further, for parallel plate capacitor, the charge of the capacitor is given by, $Q=CV$and the Electric field of the parallel plate capacitor is given by $E=Vd$.
Step by step solution:
Let’s make a more detailed diagram of the problem given.
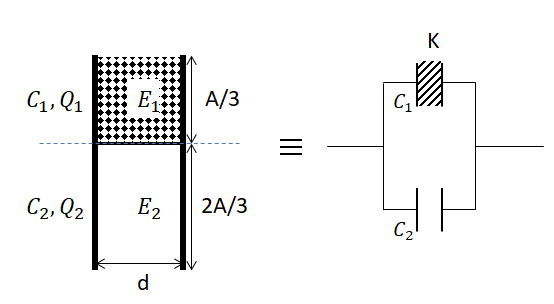
From the problem, we are given that the slab of dielectric constant (K) in between the plates, covers an area of $\dfrac{A}{3}$. The rest of the capacitor is filled with air having dielectric constant (K=1). The division of this parallel plate capacitor makes it similar to two capacitors of capacitance $\left( {{C}_{1}} \right)$and $\left( {{C}_{2}} \right)$ which are parallel to each other. Therefore the net capacitance of this parallel plate capacitor (C) is given by: $C={{C}_{1}}+{{C}_{2}}$.
The capacitance of a parallel plate capacitor of dielectric constant (K) and area in between the parallel plate capacitor (A) and the distance between the plates of the capacitor (d) is: \[C=\dfrac{K{{\in }_{0}}A}{d}\].
Therefore, the capacitance $\left( {{C}_{1}} \right)$is: ${{C}_{1}}=\dfrac{K{{\in }_{0}}\left( \dfrac{A}{3} \right)}{d}\Rightarrow {{C}_{1}}=\dfrac{K{{\in }_{0}}A}{3d}$.
Similarly, the capacitance $\left( {{C}_{2}} \right)$ is: ${{C}_{2}}=\dfrac{K{{\in }_{0}}\left( \dfrac{2A}{3} \right)}{d}\Rightarrow {{C}_{2}}=\dfrac{(1){{\in }_{0}}(2A)}{3d}\Rightarrow {{C}_{2}}=\dfrac{2{{\in }_{0}}A}{3d}$.
Therefore the ratio of these capacitance become: \[\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{\dfrac{K{{\in }_{0}}A}{3d}}{\dfrac{2{{\in }_{0}}A}{3d}}=\dfrac{K}{2}\Rightarrow \dfrac{{{C}_{2}}}{{{C}_{1}}}=\dfrac{2}{K}\].
Adding (1) on both sides of the above equation makes it: \[\dfrac{{{C}_{2}}}{{{C}_{1}}}+1=\dfrac{2}{K}+1\Rightarrow \dfrac{{{C}_{2}}}{{{C}_{1}}}+\dfrac{{{C}_{1}}}{{{C}_{1}}}=\dfrac{2}{K}+\dfrac{K}{K}\Rightarrow \dfrac{{{C}_{1}}+{{C}_{2}}}{{{C}_{1}}}=\dfrac{2+K}{K}\Rightarrow \dfrac{C}{{{C}_{1}}}=\dfrac{2+K}{K}\].
Therefore, the ratio of the capacitance of the whole capacitor, to the capacitance of part containing the dielectric slab (K) is: \[\dfrac{C}{{{C}_{1}}}=\dfrac{2+K}{K}\].
We also know that the amount of charge in a parallel plate capacitor is given$Q=CV$. In the current case, the capacitances of $\left( {{C}_{1}} \right)$and $\left( {{C}_{2}} \right)$ are both a part of the common capacitor (C). Hence, the potential (V) remains constant. Therefore: $Q\propto C$. This implies: \[\dfrac{{{Q}_{1}}}{{{Q}_{2}}}=\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{K}{2}\Rightarrow \dfrac{{{Q}_{1}}}{{{Q}_{2}}}=\dfrac{K}{2}\].
The Electric field of a parallel plate capacitor is given by, $E=Vd$. For the current case, the potential remains constant, as the capacitances $\left( {{C}_{1}} \right)$and $\left( {{C}_{2}} \right)$ are both a part of the common capacitor (C). Therefore: $E\propto d$. For this case, the distance between the plates is constant. Hence, \[\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{d}{d}=1\Rightarrow \dfrac{{{E}_{1}}}{{{E}_{2}}}=1\].
Therefore, the options A and D, are the solutions.
Note:
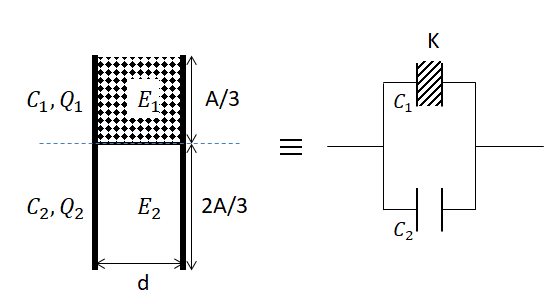
In this problem, when different dielectrics are kept in a parallel plate capacitor, horizontally one below the other, it is similar to two parallel plates capacitors being parallel to each other as in the image below.
Similarly, if there are two different dielectrics encased in a parallel plate capacitor vertically, one beside another, then it will be similar to two dielectrics in series with each other as in the image below.
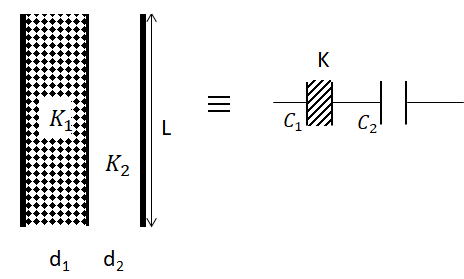
Step by step solution:
Let’s make a more detailed diagram of the problem given.

From the problem, we are given that the slab of dielectric constant (K) in between the plates, covers an area of $\dfrac{A}{3}$. The rest of the capacitor is filled with air having dielectric constant (K=1). The division of this parallel plate capacitor makes it similar to two capacitors of capacitance $\left( {{C}_{1}} \right)$and $\left( {{C}_{2}} \right)$ which are parallel to each other. Therefore the net capacitance of this parallel plate capacitor (C) is given by: $C={{C}_{1}}+{{C}_{2}}$.
The capacitance of a parallel plate capacitor of dielectric constant (K) and area in between the parallel plate capacitor (A) and the distance between the plates of the capacitor (d) is: \[C=\dfrac{K{{\in }_{0}}A}{d}\].
Therefore, the capacitance $\left( {{C}_{1}} \right)$is: ${{C}_{1}}=\dfrac{K{{\in }_{0}}\left( \dfrac{A}{3} \right)}{d}\Rightarrow {{C}_{1}}=\dfrac{K{{\in }_{0}}A}{3d}$.
Similarly, the capacitance $\left( {{C}_{2}} \right)$ is: ${{C}_{2}}=\dfrac{K{{\in }_{0}}\left( \dfrac{2A}{3} \right)}{d}\Rightarrow {{C}_{2}}=\dfrac{(1){{\in }_{0}}(2A)}{3d}\Rightarrow {{C}_{2}}=\dfrac{2{{\in }_{0}}A}{3d}$.
Therefore the ratio of these capacitance become: \[\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{\dfrac{K{{\in }_{0}}A}{3d}}{\dfrac{2{{\in }_{0}}A}{3d}}=\dfrac{K}{2}\Rightarrow \dfrac{{{C}_{2}}}{{{C}_{1}}}=\dfrac{2}{K}\].
Adding (1) on both sides of the above equation makes it: \[\dfrac{{{C}_{2}}}{{{C}_{1}}}+1=\dfrac{2}{K}+1\Rightarrow \dfrac{{{C}_{2}}}{{{C}_{1}}}+\dfrac{{{C}_{1}}}{{{C}_{1}}}=\dfrac{2}{K}+\dfrac{K}{K}\Rightarrow \dfrac{{{C}_{1}}+{{C}_{2}}}{{{C}_{1}}}=\dfrac{2+K}{K}\Rightarrow \dfrac{C}{{{C}_{1}}}=\dfrac{2+K}{K}\].
Therefore, the ratio of the capacitance of the whole capacitor, to the capacitance of part containing the dielectric slab (K) is: \[\dfrac{C}{{{C}_{1}}}=\dfrac{2+K}{K}\].
We also know that the amount of charge in a parallel plate capacitor is given$Q=CV$. In the current case, the capacitances of $\left( {{C}_{1}} \right)$and $\left( {{C}_{2}} \right)$ are both a part of the common capacitor (C). Hence, the potential (V) remains constant. Therefore: $Q\propto C$. This implies: \[\dfrac{{{Q}_{1}}}{{{Q}_{2}}}=\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{K}{2}\Rightarrow \dfrac{{{Q}_{1}}}{{{Q}_{2}}}=\dfrac{K}{2}\].
The Electric field of a parallel plate capacitor is given by, $E=Vd$. For the current case, the potential remains constant, as the capacitances $\left( {{C}_{1}} \right)$and $\left( {{C}_{2}} \right)$ are both a part of the common capacitor (C). Therefore: $E\propto d$. For this case, the distance between the plates is constant. Hence, \[\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{d}{d}=1\Rightarrow \dfrac{{{E}_{1}}}{{{E}_{2}}}=1\].
Therefore, the options A and D, are the solutions.
Note:
In this problem, when different dielectrics are kept in a parallel plate capacitor, horizontally one below the other, it is similar to two parallel plates capacitors being parallel to each other as in the image below.

Similarly, if there are two different dielectrics encased in a parallel plate capacitor vertically, one beside another, then it will be similar to two dielectrics in series with each other as in the image below.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers

State the principle of an ac generator and explain class 12 physics CBSE




