Question

A particle is moving in a circular path of radius r, its displacement after moving through half the circle would be:
A. Zero
B. r
C. 2r
D. $\dfrac{2}{r}$

Answer 1

Hint: In this question, we first see the definition of distance and displacement. After this using the concept of that displacement depends on initial and final position of the object, we will calculate the displacement of the particle in case of moving in a circular path.

Complete answer:
Let us first see the definition of distance and displacement.
Distance:
It is defined as the total distance travelled by the particle. It does not depend on the initial or final position. It just depends on the length of the path travelled. It is a scalar quantity.

Displacement:
It is defined as the change in the position of the particle as it moves from one position to another.
Mathematically, we can write:
$\vartriangle r = {r_f} - {r_i}$ , where,
$\vartriangle r$ is the displacement and ${r_f}$ and ${r_i}$ are the initial and final position of the particle.
We can also say that displacement is the shortest distance between final and initial point. It is a vector quantity.
Now, coming to question, we have a particle which has travelled half the circle and we have to find the displacement.

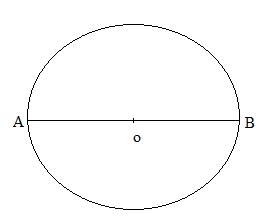
Initial position of the particle is B and the final position of the particle is A.
Therefore, the shortest distance between A and B is 2r.
Hence, displacement = 2r.

So, the correct answer is “Option C”.

Note:
In this question, you should know that definition and difference between distance and displacement. Displacement can be zero, positive or negative but distance is always positive. If the particle moves around the circle and comes to the same point then in this case displacement is zero.