
Answer
457.2k+ views
Hint: To solve this type of problem we can use conservation of momentum which states that the initial momentum of the system must be equal to the final momentum of the system. The value of unknown mass and velocity can be determined by the known value of momentum.
Complete step by step answer:
Let us first write the information given in the question.
${m_1} = 2m,{m_2} = 3m,{u_1} = \upsilon,{u_2} = 0(rest)$
The following is the diagram showing the above situation.
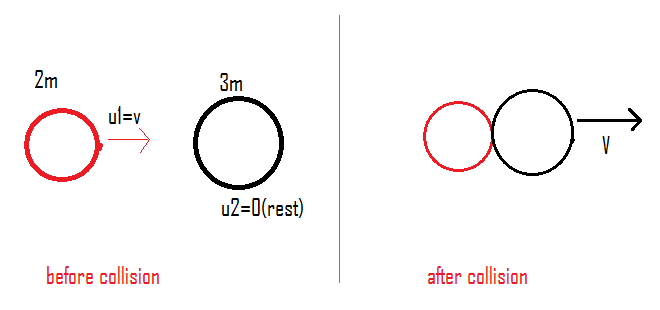
We have to find the speed of the system.
Let the speed of the system after collision is $V$.
Momentum of system before collision:
${m_1}{u_1} + {m_2}{u_2} = 2m\upsilon + 3m \times 0 = 2m\upsilon$……… (1)
Momentum of system after collision:
${m_1}{v_1} + {m_2}{v_2} = 2m \times V + 3m \times V$
Let us further simplify it.
${m_1}{v_1} + {m_2}{v_2} = 5mV$ ………. (2)
Now, let us use the concept of conservation of momentum. Equation (1) and (2) must be equal.
$2m\upsilon = 5mV$
On simplifying we get the following.
$V = \dfrac{2}{5}\upsilon= 0.4\upsilon$
$\therefore $ The speed of the system will be $0.4\upsilon$. Hence option (D) is correct.
Additional information:
- The law of conservation of momentum or the law of conservation of linear momentum states that the momentum of an isolated system remains constant. Momentum is therefore conserved over time.
- The Law of conservation holds no matter how complicated the force is between particles.
- The conservation of momentum applies to all interactions including collisions and separations caused by explosive forces.
Note:
If there are several particles, the momentum exchanged between each pair of particles adds up to zero. So that the total change in momentum is zero. The motion of the object in rest implies that the object has zero momentum. Conservation of momentum used to determine the final value velocity.
Complete step by step answer:
Let us first write the information given in the question.
${m_1} = 2m,{m_2} = 3m,{u_1} = \upsilon,{u_2} = 0(rest)$
The following is the diagram showing the above situation.
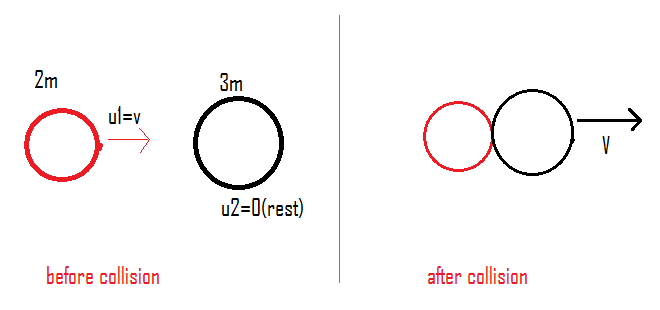
We have to find the speed of the system.
Let the speed of the system after collision is $V$.
Momentum of system before collision:
${m_1}{u_1} + {m_2}{u_2} = 2m\upsilon + 3m \times 0 = 2m\upsilon$……… (1)
Momentum of system after collision:
${m_1}{v_1} + {m_2}{v_2} = 2m \times V + 3m \times V$
Let us further simplify it.
${m_1}{v_1} + {m_2}{v_2} = 5mV$ ………. (2)
Now, let us use the concept of conservation of momentum. Equation (1) and (2) must be equal.
$2m\upsilon = 5mV$
On simplifying we get the following.
$V = \dfrac{2}{5}\upsilon= 0.4\upsilon$
$\therefore $ The speed of the system will be $0.4\upsilon$. Hence option (D) is correct.
Additional information:
- The law of conservation of momentum or the law of conservation of linear momentum states that the momentum of an isolated system remains constant. Momentum is therefore conserved over time.
- The Law of conservation holds no matter how complicated the force is between particles.
- The conservation of momentum applies to all interactions including collisions and separations caused by explosive forces.
Note:
If there are several particles, the momentum exchanged between each pair of particles adds up to zero. So that the total change in momentum is zero. The motion of the object in rest implies that the object has zero momentum. Conservation of momentum used to determine the final value velocity.
Recently Updated Pages
Who among the following was the religious guru of class 7 social science CBSE

what is the correct chronological order of the following class 10 social science CBSE

Which of the following was not the actual cause for class 10 social science CBSE

Which of the following statements is not correct A class 10 social science CBSE

Which of the following leaders was not present in the class 10 social science CBSE

Garampani Sanctuary is located at A Diphu Assam B Gangtok class 10 social science CBSE

Trending doubts
A rainbow has circular shape because A The earth is class 11 physics CBSE

Which are the Top 10 Largest Countries of the World?

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

What was the Metternich system and how did it provide class 11 social science CBSE

How do you graph the function fx 4x class 9 maths CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is BLO What is the full form of BLO class 8 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




