Question

A particle of specific charge $\alpha $ is projected from origin with velocity${\vec v_0} = {v_0}\hat i - {v_0}\hat k$ in a uniform magnetic field $\vec B = - {B_0}\hat k$. Find time dependence of velocity of the particle :
A. $\vec v(t) = {v_0}\cos (\alpha {B_0}t)\hat i + {v_0}\sin (\alpha {B_0}t)\hat j - {v_0}\hat k$
B. $\vec v(t) = - {v_0}\cos (\alpha {B_0}t)\hat i + {v_0}\sin (\alpha {B_0}t)\hat j + {v_0}\hat k$
C. $\vec v(t) = - {v_0}\cos (\alpha {B_0}t)\hat i + {v_0}\sin (\alpha {B_0}t)\hat j - {v_0}\hat k$
D. $\vec v(t) = {v_0}\cos (\alpha {B_0}t)\hat i + {v_0}\sin (\alpha {B_0}t)\hat j + {v_0}\hat k$

Answer 1

Hint: Magnetic field is directed into the plane that is along the negative$z$ axis, we know a magnetic field makes a charged particle move in a circle. We are given initial velocity of particle and we need to find velocity of particle as a function of time.

Formula used:
$\theta = \omega t$
$r = \dfrac{{mv}}{{\alpha {B_0}}}$

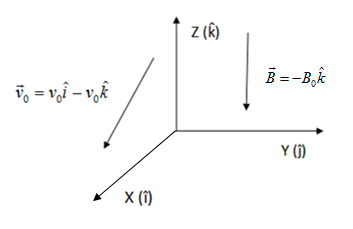
The diagram shows the right hand axes system in which direction of unit vector $\hat i$ is along $x$ axis, direction of unit vector $\hat j$ along $y$ axis and direction of unit vector $\hat k$ along $z$ axis. Also suggests direction of magnetic field vector and velocity vector.

Complete answer:
As the magnetic field is directed into the plane that is along the negative $z$ axis the particle will perform circular motion in the $xy$ plane, also the particle has a component of initial velocity along the $z$ direction the particle will have a helical path. Now we know that the effect of the magnetic field will be only along the component of velocity perpendicular to it. The motion of the particle will be in three dimensions so the final velocity of the particle will have components along the $x,y$ and $z$ axis.

Since the particle will be performing circular motion in $xy$ plane the component of velocity of particle along $x$ and $y$ axis can be taken as $v{}_0\cos \theta $ and ${v_0}\sin \theta $ where $\theta $ is the angle between velocity of particle and $x$ axis. Velocity of the particle will remain unchanged along the $z$ axis. Now the particle will revolve in a circle of radius $r$, and we know the formula to calculate $r$, which is $r = \dfrac{{mv}}{{\alpha {B_0}}}$ for a particle of unit mass $r = \dfrac{v}{{\alpha {B_0}}}$ ,
On rearranging we get: $\dfrac{v}{r} = \alpha {B_0}$
Also we know for a particle revolving in a circle $\theta = \omega t$ but $\omega $ is also equal to $\dfrac{v}{r}$
Than, $\alpha B = \dfrac{\theta }{t}$ or $\theta = \alpha {B_0}t$
So the horizontal component of velocity of a particle is ${v_0}\cos (\alpha {B_0}t)$. Vertical component is${v_0}\sin (\alpha {B_0}t)$ and the component of velocity along the $z$ axis remains unchanged.
So time dependence of velocity of particle is ${v_0}\cos (\alpha {B_0}t)\hat i + {v_0}\sin (\alpha {B_0}t)\hat j - {v_0}\hat k$

So, the correct answer is “Option A”.

Note:
Any charged particle will be affected by magnetic field only if it has a component of velocity perpendicular to direction of magnetic field, while doing calculations always take only the component of velocity which is perpendicular to direction of magnetic field.