Question

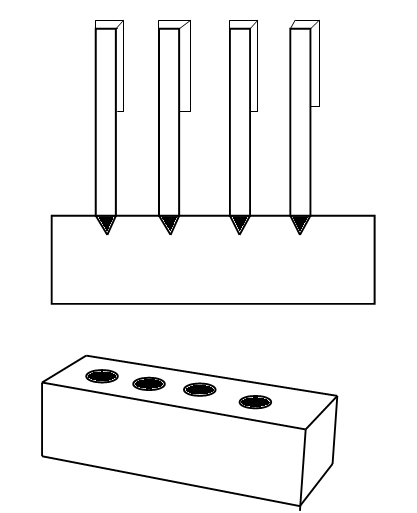
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold Pens. The dimensions of the cuboid are 15cm by 10cm by 3.5 cm . The radius of each of the depression is 0.5cm and the depth is 1⋅4cm .Find the volume of the wood in the entire stand. \[\]

Answer 1

Hint: We find the volume of the stand as $ V={{V}_{1}}-4{{V}_{2}} $ where $ {{V}_{1}} $ is the volume of the cuboid without depressions and $ {{V}_{2}} $ is the volume of the conical depressions. We find the volume of cuboid using the formula $ {{V}_{1}}=l\times b\times h $ where $ l,b,h $ are the length, breadth and height of the cuboid. We find $ {{V}_{2}}=\dfrac{1}{3}\pi {{r}^{2}}h $ where $ r $ the radius of depression and $ h $ is the depth. \[\]

Complete step by step answer:
We know that a cuboid is a three-dimensional object with six rectangular faces joined by 8 vertices. It has three different types of sides called length, breadth and height denoted $ l, $ $ b $ and $ h $ respectively. So the volume of the cuboid is given by;

\[{{V}_{\text{cuboid}}}=l\times b\times h\]

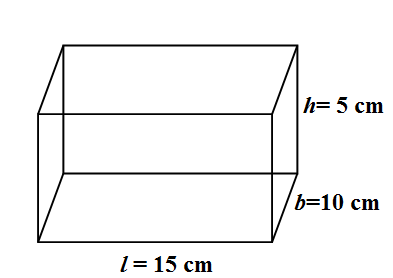
We are given the question that the wooden pen stand is in the shape of a cuboid with The dimensions of the cuboid are 15cm by 10cm by 3.5 cm. So let us assign $ l=15,b=10,h=3.5 $ . \[\]

So the volume of the cuboid is
\[{{V}_{1}}=15\times 10\times 3.5=525\text{ c}{{\text{m}}^{3}}\]
We know from the right circular cone that the line segment joining the apex to the center is the height of the cone denoted as $ h $ . the volume of a cone with radius at the base $ r $ and height $ h $ is given by
\[{{V}_{2}}=\dfrac{1}{3}\pi {{r}^{2}}h\]
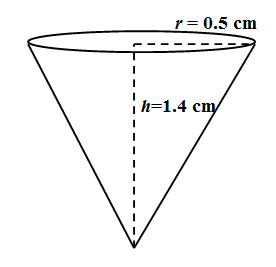
We see that there are 4 conical depressions on the wooden pen stand. We are given that the radius of each of the depressions is 0.5cm and the depth is 1⋅4cm. Here the radius of the depression is the radius of the base that is $ r=0.5 $ cm and the height of the cone is the depth of the depression that is $ h=1.4 $ cm. \[\]
 So volume of one conical depression is ;
\[\begin{align}
  & {{V}_{2}}=\dfrac{1}{3}\pi {{r}^{2}}h \\
 & \Rightarrow {{V}_{2}}=\dfrac{1}{3}\times 3.14\times {{\left( 0.5 \right)}^{2}}\times 1.4 \\
 & \Rightarrow {{V}_{2}}=0.3663\text{ c}{{\text{m}}^{3}} \\
\end{align}\]
So the volume of the wooden pen stand volume of the cuboid minus the volumes of 4 conical depressions that is
\[V={{V}_{1}}-4{{V}_{2}}=525-1.4665=523.535\text{ c}{{\text{m}}^{3}}\]
Note:
 We have taken the value of $ \pi $ here as 3.14 , we can also take $ \pi =\dfrac{22}{7} $ . If we want to approximate up to two decimals we have to take $ \pi =3.141 $ . We can also find the surface area of the top surface as $ l\times b-4\times \pi {{r}^{2}} $ . If we are not given the height of the cone but slant height $ l $ is given , we can find the volume as $ V=\dfrac{1}{3}\pi {{r}^{2}}\sqrt{{{r}^{2}}+{{l}^{2}}} $ .We should take care of the units during calculation.