Question

A pendulum is hanging from the ceiling of a cage. If the cage moves up with constant acceleration a, its tension is $ {T_1} $ ​ and if it moves down with the same acceleration, the corresponding tension is $ {T_2} $ ​. The tension in the string if the cage moves horizontally with same acceleration $ a $ is

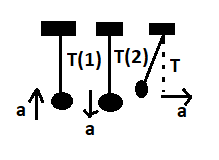
(A) $ \dfrac{{\sqrt {T_1^2 + T_2^2} }}{2} $
(B) $ \dfrac{{\sqrt {T_1^2 - T_2^2} }}{2} $
(C) $ \sqrt {\dfrac{{T_1^2 + T_2^2}}{2}} $
(D) None of the above

Answer 1

Hint
We draw the free-body diagrams for the three cases. We find the tension in all three cases with the help of the free body diagram. Adding the square of tension (1) and tension (2) we get an equation equal to that of the tension in the third case. Further simplifying we get the relation between all the three tensions.

Complete step by step answer
The free-body diagrams of the three pendulums are

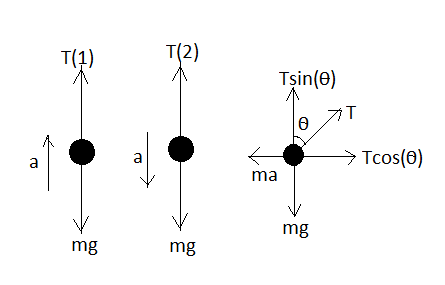
From the free-body diagrams of pendulum 1, pendulum 2, pendulum 3
The force acting on the pendulum due to acceleration is the difference between the tension force and the weight.
The tension in pendulum one is
 $ {T_1} - mg = ma $
 $ \Rightarrow {T_1} = m\left( {g + a} \right)\; $
 $ \Rightarrow \dfrac{{{T_1}}}{m} = g + a.....(1) $
The tension in pendulum 2 is
 $ {T_2} - mg = - ma $
 $ \Rightarrow {T_2} = m\left( {g - a} \right)\; $
 $ \Rightarrow \dfrac{{{T_2}}}{m} = g - a.....(2) $
When the cage moves horizontally with an acceleration $ a $ , let the tension be $ \;T $ .
From the free body diagram,
 $ \Rightarrow T\cos\theta = ma $
 $ \Rightarrow \;T\sin\theta =mg $
Squaring and adding the above equations,
 $ \Rightarrow {\left( {T\sin\theta } \right)^2} + {\left( {T\cos\theta } \right)^2} = {\left( {ma} \right)^2} + {\left( {mg} \right)^2} $
 $ (\because {\sin ^2}(\theta ) + {\cos^2}(\theta ) = 1) $
 $ \Rightarrow {T^2} = {m^2}\left( {{g^2} + {a^2}} \right)\; .....(3) $
Squaring (1) and (2) and adding
 $ {\left( {\dfrac{{{T_1}}}{m}} \right)^2} + {\left( {\dfrac{{{T_2}}}{m}} \right)^2} = {\left( {g + a} \right)^2} + {\left( {g - a} \right)^2} $
 $ \because{(a + b)^2} - {(a - b)^2} = 2({a^2} + {b^2}) $
 $ \Rightarrow \dfrac{{{T_1}^2 + T_2^2}}{{{m^2}}} = 2({g^2} + {a^2}) $
 $ \Rightarrow \dfrac{{T_1^2 + T_2^2}}{2} = \left( {{g^2} + {a^2}} \right){m^2}\;.....(4) $
Equations (3) and (4) are equal, equating (3) and (4)
 $ {T^2} = \dfrac{1}{2}(T_1^2 + T_2^2) $
 $ \Rightarrow T = \sqrt {\dfrac{1}{2}(T_1^2 + T_2^2)} $
Hence the tension in pendulum three is $ T = \sqrt {\dfrac{1}{2}(T_1^2 + T_2^2)} $
Option (B) $ T = \sqrt {\dfrac{1}{2}(T_1^2 + T_2^2)} $ is the correct answer.

Additional Information
Tension is defined as a pulling force transmitted axially by a rope, string, chain, and rod. A good elastic material can withstand a greater tension force without breaking.

Note
Students may get confused to find if a force is positive or negative. While solving the problem we have considered all the forces acting upwards as positive and all the forces acting downwards as negative, which uses nothing but adding all the forces acting in the direction and subtracting them with the forces acting in the opposite direction.