Question

A person cannot see distant objects beyond 2m. This defect can be corrected by using a lens of power:
A. +0.5 D
B. -0.5 D
C. +0.2 D
D. -0.2 D

Answer 1

- Hint: The maximum distance up-to which a person can see clearly is called his far point and the minimum distance up-to which a person can see properly is called near point. Due to some defect in the eye with age, many people have problems with vision. This results in long sightedness or short sightedness of a person.

Complete step-by-step solution -
Formula used: Lens formula:$\dfrac 1f= \dfrac 1v- \dfrac 1u$, $P= \dfrac1f$

Person’s long sightedness is affected means the rays coming from a longer distance are unable to get focused on the retina of his eye. This means his eye is defected in such a way that the eye is bending the rays with more power. As far as his near sight is concerned, the lens is unable to converge because rays coming from a shorter distance are much more divergent than far rays.
Hence this can be resolved by diverging the far rays either. This could only be done by placing a diverging lens (or concave lens) before his eyes.
 

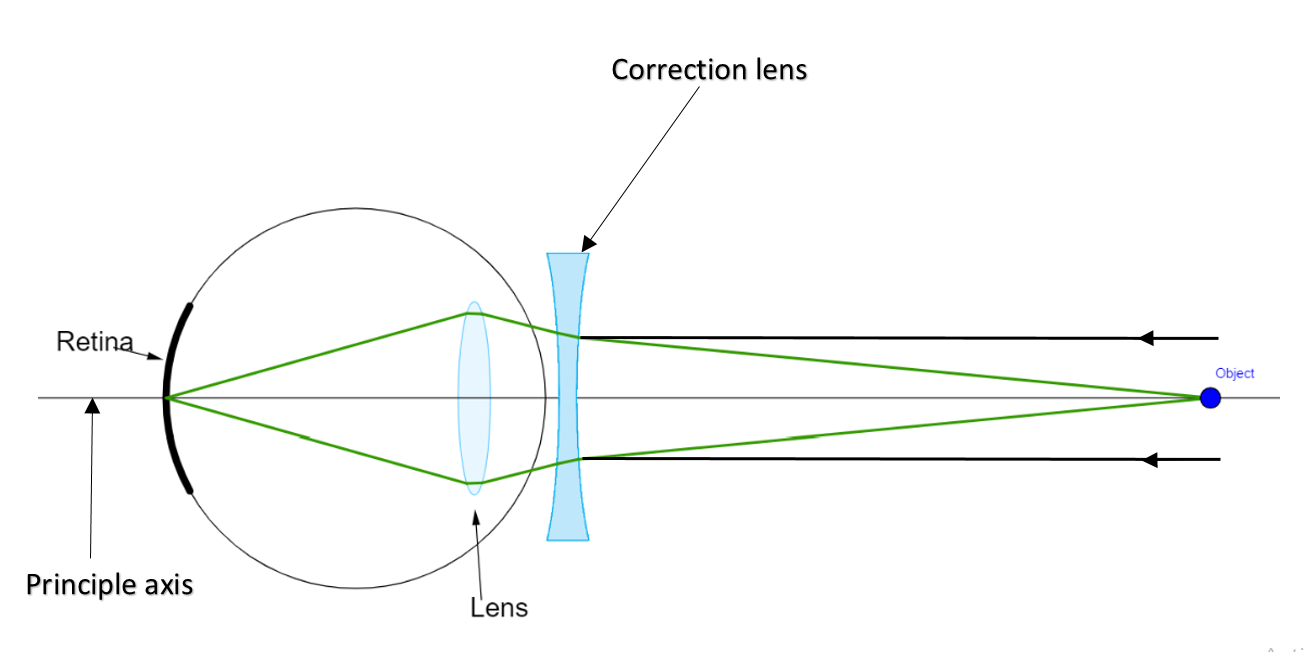
Now, we wanted to correct his vision for far rays, hence u = -∞ and v = -2m
Using lens formula:
$\dfrac 1f= \dfrac 1v- \dfrac 1u$ = $\dfrac{1}{-2}-\dfrac{1}{-\infty }$= $\dfrac 1{-2}$ [ $\dfrac{1}{\infty }\to 0$]
Or f = -2m
Hence $P= \dfrac1f$= $\dfrac 1{-2} = -0.5D$
Hence option B. is correct.

Note: In optics lens and mirror problems, the first and foremost thing is to understand the sign conventions properly and then proceed, otherwise the topic will seem very difficult. Students are also advised to understand the diagrams of image formation in various cases of lens and mirror.