Question

A person is looking at the flat surface of a transparent hemisphere of refractive index\[\mu =\sqrt{2}\]. Half of the flat surface is coloured black and half of curved surface is coloured in six equally spaced strips as shown in figure

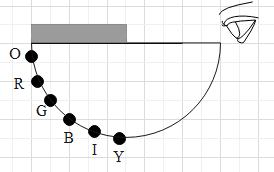
(This question has multiple correct option)
A. the person can see green, orange and red.
B. the person can see only yellow, indigo and blue.
C. The ray coming from red and orange stripes will be totally reflected.
D. the ray coming from yellow, indigo and blue stripes will be totally reflected.

Answer 1

Hint: Here refraction of light is happening, i.e. when light travels from vacuum to the flat surface, medium changes and light rays bends while changing its path. But the light ray can get refracted at a certain limit after that it gets totally reflected to the same medium it travelled from. Here we will discuss the phenomenon of refraction in brief and from that we will get our answer.

Formula used:
\[\sin {{i}_{c}}=\dfrac{1}{\mu }\]

Complete step-by-step answer:
In refraction of light, when light travels from denser to rarer medium or rarer to denser medium the rays will get refracted i.e. it bends away or towards the normal. Normal is an imaginary line taken perpendicular to the medium. But after a particular angle light will be reflected back to the same medium, the angle at which the light ray gets reflected back to the medium it was coming from is known as the critical angle of incidence. Critical angle for light travelling from denser to rarer medium is given as
\[\sin {{i}_{c}}=\dfrac{1}{\mu }\]
Here, the light is travelling from denser to rarer (vacuum), hence by substituting the value of the refractive index we will get the critical angle.
\[\begin{align}
  & \sin {{i}_{c}}=\dfrac{1}{\sqrt{2}} \\
 & {{i}_{c}}=\sin {{\left( \dfrac{1}{\sqrt{2}} \right)}^{-1}} \\
 & {{i}_{c}}=45{}^\circ \\
\end{align}\]
The critical angle for the transparent hemisphere is \[45{}^\circ \], for an angle of incidence greater or equal to critical angle, light will get totally reflected back.
Now let us consider the figure given and draw a normal and the critical angle

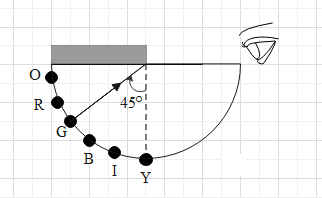
We can see for the green strip the angle of incidence is the same as critical angle. For orange and red angles of incidence will be greater than the critical angle. Therefore for orange, red and green stripes the ray will get totally reflected. Whereas, for yellow, indigo and blue stripes angle of incidence is smaller than critical angle and we get a refracted ray. Therefore people will see the yellow, indigo and blue stripes.

So, the correct answers are “Option B and C”.

Note: The given question has multiple correct options that means one or more than one option can be right.
In case the ray travels from rarer to denser medium the critical angle will be given as the sine of critical angle will be equal to the refractive index. Also note that angle of incidence is taken from normal towards the plane.