Question

A Plano concave lens is made of glass of refractive index $1.5$ and the radius of curvature of its curved face is $100cm$. What will be the power of the lens?
$\begin{align}
 & A.+0.5D \\
 & B.-0.5D \\
 & C.-2D \\
 & D.+2D \\
\end{align}$

Answer 1

Hint: The power of a lens is described as the reciprocal of the focal length. Lens power is usually determined in dioptres which is abbreviated as D. Converging or the convex lenses are having positive focal lengths, hence they are also having positive power values. Diverging otherwise called concave lenses have negative focal lengths, hence they also are having negative power values.

Complete step by step answer:
First of all let us discuss what the power of a lens means. It is the reciprocal of focal length.
Lens surface power can be determined with the index of refraction and also the radius of curvature.

It is given by the equation,

$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$
Where ${{R}_{1}}$ and ${{R}_{2}}$ is the radius of curvature of the two sides of a lens.
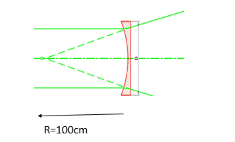
So here it has been given that the lens used up is a Plano concave lens.
Therefore for the plane surface the radius of curvature will be infinity.
${{R}_{1}}=\infty $

And the other surface is concave with a radius of curvature $100cm$

Therefore\[\dfrac{1}{f}=-\dfrac{0.5}{100}cm=-0.5m\]
${{R}_{2}}=100cm$

An also refractive index is,
$\mu =1.5$
Substituting these all in the lens maker's equation,
$\dfrac{1}{f}=\left( 1.5-1 \right)\left( \dfrac{1}{\infty }-\dfrac{1}{100} \right)$
Simplifying this,
$\dfrac{1}{f}=-\dfrac{0.5}{100}cm=-0.5m$
As we all know the power of a lens means,
$D=\dfrac{1}{f}$

Hence the power of the plano concave lens given in the question is -0.5D.
Therefore the correct answer for this question is option B.
Hence, the correct answer is option B.

Note:
The power of a lens is explained as the reciprocal of its focal length in meters,
The equation for finding out the power of a lens is,
$D=\dfrac{1}{f}$
Where D is the power of the lens in dioptres and f is the focal length of the lens in meters.