Question

A power transformer (step-up) with a 1:8 turn ratio has 60 Hz, 120 V across the primary; the load in the secondary is ${{10}^{4}}\,\Omega $. The current in the secondary is

Answer 1

Hint: A transformer operates on Faraday’s principle of mutual inductance between two coils, primary and secondary coil. The voltages across either coil are directly proportional to the number of turns in the respective coils.

Complete step by step answer:
A transformer is an electrical device used to increase or decrease the RMS voltage of an input AC source. It consists of two insulated coils (primary coil and secondary coil) operating on Faraday’s principle of mutual inductance. What happens is that when an alternating voltage is applied in the primary coil, it acts like an electromagnet that generates an alternating magnetic field. The alternating magnetic field interacts with the secondary coil; an EMF is induced in the secondary coil due to the alternating magnetic flux of the primary coil.

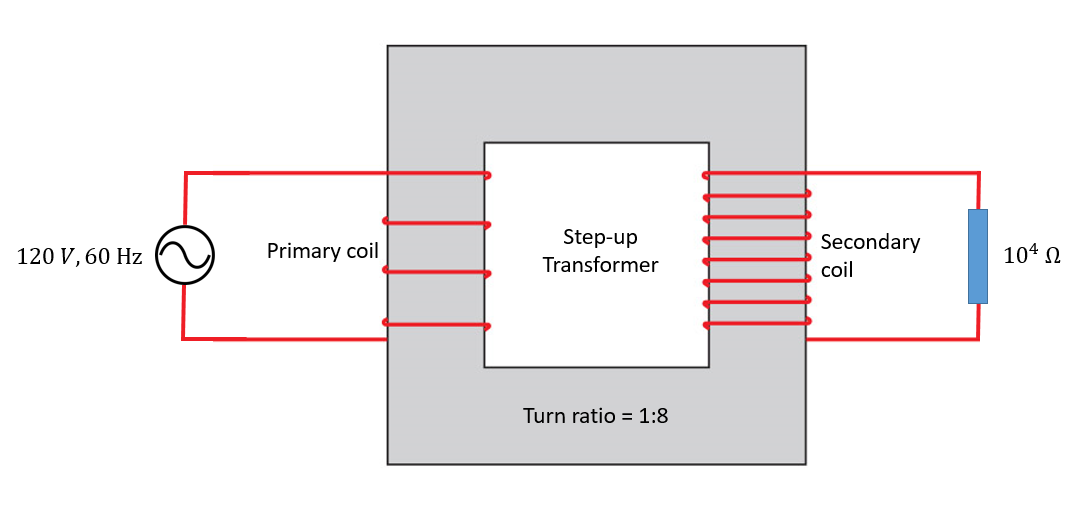
A step-up transformer is a type of transformer, which amplifies (or, increases) a low input alternating voltage (or, high alternating current) and supplies a high output alternating voltage (or, low alternating current). This is achieved when the secondary coil has a greater number of turns as compared to the primary coil. Therefore, the alternating voltages at either end of the coil are associated with the ratio of the number of turns of either coil. So we can write
$\dfrac{{{N}_{P}}}{{{N}_{S}}}=\dfrac{{{V}_{P}}}{{{V}_{S}}}$ [known as Transformer formula]
Where, ${{N}_{P}}$ and ${{N}_{S}}$ are the number of turns of primary and secondary coils, respectively, and ${{V}_{P}}$ and ${{V}_{S}}$ are the voltages across primary and secondary coils, respectively. Since in the question we are provided with the turn ratio $({{N}_{P}}:{{N}_{S}}=1:8)$ and the voltage across the primary coil ${{V}_{P}}=120\,\text{V}$, then from the above formula the voltage across the secondary coil will be
$\begin{align}
& \dfrac{1}{8}=\dfrac{120\,V}{{{V}_{S}}} \\
& \therefore \,{{V}_{S}}=960\,V \\
\end{align}$
Since the load resistance connected across the secondary coil is ${{10}^{4}}\,\Omega $, then according to Ohm’s law, the current in the secondary coil will be
$\begin{align}
& {{I}_{S}}=\dfrac{{{V}_{S}}}{{{R}_{S}}} \\
& {{I}_{S}}=\dfrac{960\,V}{{{10}^{4}}\,\Omega } \\
& {{I}_{S}}=0.096\,A \\
& \therefore \,{{I}_{S}}=96\,mA \\
\end{align}$

Hence, the current in the secondary coil is 96 mA.

Note:
The EMF induced (${{V}_{ind}}$) in a coil of N turns is given by
${{V}_{ind}}=-N\dfrac{d\Phi }{dt}$
Where $\dfrac{d\Phi }{dt}$is the rate of change of magnetic flux. In the above case, the induced voltage in the secondary coil ${{V}_{S}}$ can be expressed as
${{V}_{S}}=-{{N}_{S}}\dfrac{d{{\Phi }_{SP}}}{dt}$ ………. (1)
Where, $\dfrac{d{{\Phi }_{SP}}}{dt}$is the rate of flux change in the secondary coil due to the primary coil. Similarly, the voltage in the primary coil can be expressed as
${{V}_{P}}=-{{N}_{P}}\dfrac{d{{\Phi }_{PS}}}{dt}$ ………. (2)
Where, $\dfrac{d{{\Phi }_{PS}}}{dt}$ is the rate of flux change in the primary coil due to the secondary coil. In mutual inductance, the flux linked between the two coils are same, therefore
\[\dfrac{d{{\Phi }_{SP}}}{dt}=\dfrac{d{{\Phi }_{PS}}}{dt}=\dfrac{d\Phi }{dt}\]
Therefore, equation 1 and 2 becomes
${{V}_{S}}=-{{N}_{S}}\dfrac{d{{\Phi }_{{}}}}{dt}$ ……….. (3)
${{V}_{P}}=-{{N}_{P}}\dfrac{d{{\Phi }_{{}}}}{dt}$ ……….. (4)
From Eqs. 3 and 4 we can say, in mutual inductance ${{V}_{S}}\propto \,{{N}_{S}}\text{ and }{{V}_{P}}\propto \,{{N}_{p}}$. Now, dividing equation 4 by 3, we get
\[\begin{align}
& \Rightarrow \dfrac{{{V}_{P}}}{{{V}_{S}}}=\dfrac{-{{N}_{P}}\dfrac{d\Phi }{dt}}{-{{N}_{S}}\dfrac{d\Phi }{dt}} \\
 & \Rightarrow \dfrac{{{V}_{P}}}{{{V}_{S}}}=\dfrac{{{N}_{P}}}{{{N}_{S}}} \\
\end{align}\]
Which is the transformer formula.