Question

A proton and a deuteron, each moving with velocity $ \vec v $ enter simultaneously in the region of the magnetic field $ \vec B $ acting normal to the direction of velocity. Trace their trajectories establishing between the two.

Answer 1

Hint :For a particle entering a magnetic field applied perpendicular to the direction of velocity, the particle traces a circular path inside the magnetic field. The radius of this circular path depends on the charge and mass of the particle.

Complete Step By Step Answer:
We know that a deuteron is a particle composed of a proton and a neutron.
From the given data, we can understand that,
Charge of proton = $ e $
Charge of deuteron = $ e $ ( $ \because $ neutron is chargeless)
Mass of proton = $ m $
Mass of deuteron = $ 2\;m $ ( $ \because $ mass of neutron and proton is same)
From the theory of cyclotron, we can understand that if a particle moving with velocity $ \vec v $ enters a magnetic field $ \vec B $ that is applied perpendicular to the direction of velocity, the particle traces a circular path.
The force applied by the magnetic field can be expressed as $ F = qvB $
Where $ q $ is the charge of the particle
 $ v $ is the velocity of the particle and
 $ B $ is the magnitude of the magnetic field applied.
Now, for the given data, we know that charge of both the particles is the same, the moving velocity is also the same, and the applied magnetic field is also the same.
Thus the magnetic force acting on both the particles is the same.
Now, we know that the required magnetic force is provided by the centripetal force, which is generated due to circular motion
The centripetal force is given as $ {F_c} = \dfrac{{m{v^2}}}{r} $
Where $ m $ is the mass of the particle
 $ v $ is the magnitude of the velocity of the particle and
 $ r $ is the radius of the circular path traced by the particle
Now, as the magnetic force for the given particles is the same, the centripetal forces can be compared as,
 $ \dfrac{{{m_p}{v^2}}}{{{r_p}}} = \dfrac{{{m_d}{v^2}}}{{{r_d}}} $
The mass of the deuteron is double the mass of a proton.
 $ \therefore \dfrac{{{m_p}}}{{{r_p}}} = \dfrac{{2{m_p}}}{{{r_d}}} $
The ratio of the radius of the path for deuteron to the radius for proton is,
 $ \therefore \dfrac{{{r_d}}}{{{r_p}}} = 2 $
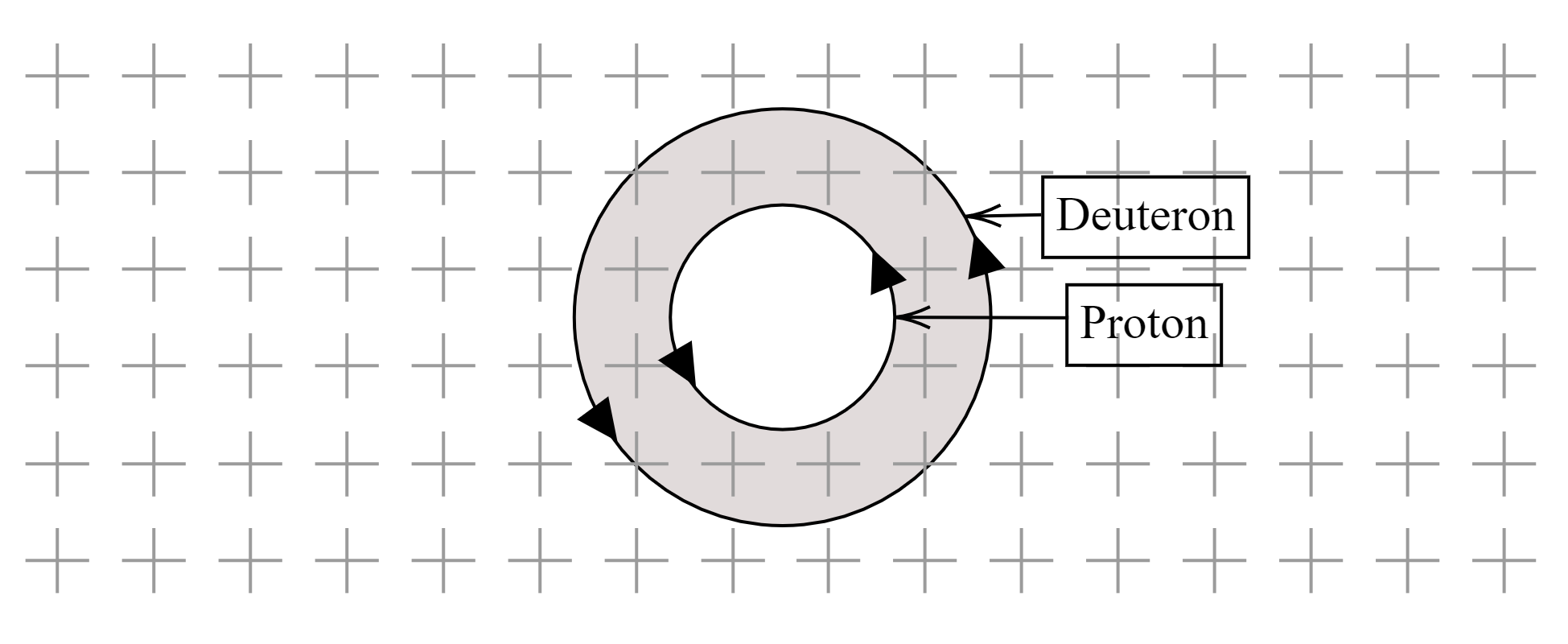
Hence, the circle traced by the deuteron particle is double the radius of the circle traced by the proton.
The trajectories for both particles can be shown as,

Note :
The force on the particle due to the magnetic field is perpendicular to the velocity at every point in the magnetic field. Hence, only the direction of velocity changes, but the magnitude remains constant for both particles.